Анализ точности электронных средств. Работы по вероятностно-статистическим методам анализа, страница 3

где 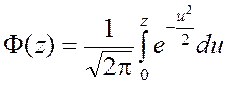   – табулированная функция (см. приложение, табл. П1).

В качестве меры расхождения  принимается сумма квадратов отклонений (), взятых с некоторыми "весами" . "Веса" разрядов вводятся потому, что отклонения, относящиеся к разным разрядам, нельзя считать равноправными по значимости: одно и то же по абсолютной величине отклонение () может быть малозначительным, если сама вероятность  велика, и очень существенным, если она мала.

С учётом "весов" мера отклонения, обозначаемая через c², будет определяться по формуле

.

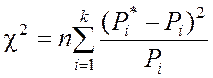Если ввести n под знак суммы и учесть, что  ,                 где m_i – число попаданий случайной величины в i-й разряд, выражение c² можно привести к виду

.

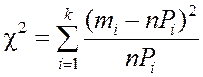Распределение c² зависит от параметра r, называемого числом "степеней свободы". Последнее равно количеству разрядов k минус количество независимых условий  s ("связей"), накладываемых на частоты   

r = k – s.

Такие независимые условия:

1. 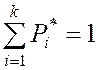  (накладывается во всех случаях);

2.  ;

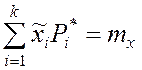3. 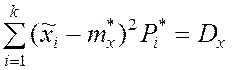  и другие моменты высших порядков.

Второе и третье условия накладываются, когда числовые характеристики теоретического распределения m_x и D_x принимаются равными соответствующим статистическим значениям.

Для полученного значения c² и числа степеней свободы r по специальным таблицам П2 находится вероятность P того, что за счёт чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем фактически наблюдаемое в данной серии опытов значение c².

Если величина P мала (меньше 0,1), то принятое теоретическое распределение следует считать несоответствующим действительному распределению величины X. Напротив, если вероятность P сравнительно велика (больше 0,8), можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счёт случайных причин. Принятое теоретическое распределение считается в этом случае не противоречащим опытным данным.

Заметим, что при использовании критерия c² должно быть большим не только общее число опытов n, но и число наблюдений m_i в отдельных разрядах (не менее 5 – 10).

Полученные статистические значения  и  всегда будут содержать элемент случайности и, следовательно, отличаться от истинных значений. Причём, ошибка будет тем меньше, чем больше число опытов. Точность и  достоверность полученных значений m_xи D_x оцениваются так называемыми доверительными интервалами и доверительной вероятностью. Эти понятия будут рассмотрены в следующих лабораторных работах.

Порядок выполнения работы

1. Измерить величину параметра радиоэлемента в заданной партии, состоящей из 100 – 150 штук (по указанию преподавателя).

2. По данным измерений построить статистический ряд.

3. Определить статистическое математическое ожидание и дисперсию.

4. Построить гистограмму.

5. Подобрать теоретическую кривую плотности распределения и провести оценку согласованности этой кривой и статистического распределения по критерию c².

Задание на подготовку к работе

1. Ознакомиться с методами обработки статистических данных.

2. Составить таблицы для записи результатов измерений.

3. Ознакомиться с техническими характеристиками универсально-измери-тельного прибора, используемого в работе, и правилами работы с ним (см. приложение).

Лабораторное задание

1. Измерить величину параметра радиоэлемента в партии, состоящей из 100 – 150 штук.

2. Обработать полученные данные в соответствии с «МЕТОДИЧЕСКИМИ УКАЗАНИЯМИ».

Содержание отчёта

1. Цель работы.

2. Тип элемента и его номинальное значение; тип и номер измерительного прибора.

3. Измеренные значения параметров элементов.

4. Статистический ряд, гистограмма и теоретическая кривая.

5. Оценка согласованности статистического и теоретического распределений при помощи критерия c².

6.  Выводы.

Контрольные вопросы