Если качество работы радиоизделия определяется несколькими параметрами, то составляется система уравнений погрешностей, число уравнений в которой равно количеству основных выходных параметров.
При расчете допусков в уравнения (2) или (3) вместо погрешностей
необходимо подставлять характеристики поля допуска. К ним относятся: величина
поля допуска ![]() , координата его середины
, координата его середины ![]() , половина поля допуска
, половина поля допуска ![]() . При вероятностном методе расчета необходимо
знать вид закона распределения погрешностей
. При вероятностном методе расчета необходимо
знать вид закона распределения погрешностей 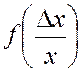 и его
числовые характеристики.
и его
числовые характеристики.
На рис. 1 изображены характеристики для случая, когда среднее значение
относительной погрешности смещено от номинала в положительную сторону, что не
влияет на общность рассуждений. Очевидно, предельное отклонение искомого
выходного параметра ![]() можно найти по формуле
можно найти по формуле
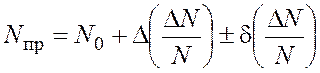 .
.
При методе предельных отклонений значения 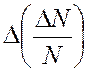 и
и 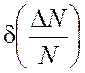
 определяются отношениями
определяются отношениями
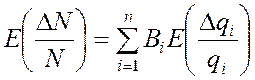 ;
;
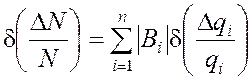 , полученными на
основе выражения (3).
, полученными на
основе выражения (3).
При расчете допусков вероятностным методом целесообразно использовать числовые
характеристики законов распределения погрешностей, установив связь между этими
характеристиками поля допуска, например, половиной поля допуска ![]() и координатой середины поля допуска
и координатой середины поля допуска ![]() .
.
Такая связь устанавливается соотношением
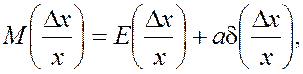
где ![]() – коэффициент относительной асимметрии
распределения отклонений в поле допуска,
– коэффициент относительной асимметрии
распределения отклонений в поле допуска, 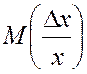 -
математическое ожидание.
-
математическое ожидание.
Используя это выражение и правила суммирования математических ожиданий и
дисперсией, на основе уравнения (3) получим формулы для определения 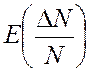 и
и 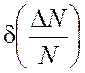 :
:
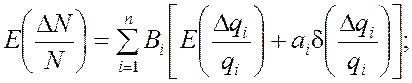 (5)
(5)
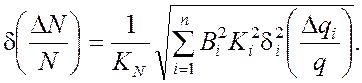 (6)
(6)
Здесь К – коэффициент относительного рассеивания, определяемый по формуле
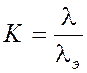 , где
, где 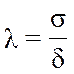 – относительное рассеивание погрешностей
параметра;
– относительное рассеивание погрешностей
параметра;
![]() – среднее квадратическое отклонение
погрешностей;
– среднее квадратическое отклонение
погрешностей;
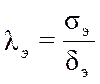 – относительное рассеивание эталонного
нормального распределения с центром группирования, совпадающим с серединой поля
допуска и при
– относительное рассеивание эталонного
нормального распределения с центром группирования, совпадающим с серединой поля
допуска и при 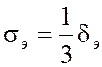 .
.
Если распределение погрешностей параметра подчиняется нормальному закону,
то при значениях 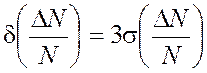 в пределах поля допуска
содержится 99,73 % всех отклонений параметра от номинального значения. Другими
словами, вероятность того, что значение выходного параметра будет находиться в
пределах поля допуска, равна 0,9973. Коэффициент относительного рассеивания
в пределах поля допуска
содержится 99,73 % всех отклонений параметра от номинального значения. Другими
словами, вероятность того, что значение выходного параметра будет находиться в
пределах поля допуска, равна 0,9973. Коэффициент относительного рассеивания ![]() равен единице. Для других значений
вероятности величина
равен единице. Для других значений
вероятности величина ![]() может быть рассчитана или взята
из таблицы [3].
может быть рассчитана или взята
из таблицы [3].
Выражение (6) справедливо для некоррелированных погрешностей параметра ![]() , в противном случае половина поля допуска
вычисляется по формуле
, в противном случае половина поля допуска
вычисляется по формуле
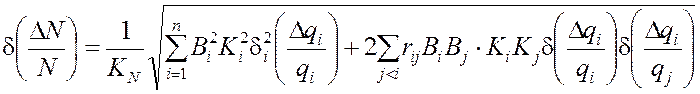 . (7)
. (7)
Здесь по ![]() суммируются все независимые и
коррелятивно зависимые погрешности, а по
суммируются все независимые и
коррелятивно зависимые погрешности, а по ![]() – пары
погрешностей, связанные функциональной или коррелятивной зависимостью, которая
определяется коэффициентом корреляции
– пары
погрешностей, связанные функциональной или коррелятивной зависимостью, которая
определяется коэффициентом корреляции ![]() .
Значение коэффициента находится на основе паспортных данных или статистически.
.
Значение коэффициента находится на основе паспортных данных или статистически.
При расчете допусков необходимо знать коэффициенты влияния ![]() , которые определяются методами
расчетно-аналитическим, малых приращений и на основе планируемого эксперимента и корреляционного анализа.
, которые определяются методами
расчетно-аналитическим, малых приращений и на основе планируемого эксперимента и корреляционного анализа.
Расчетно-аналитический метод применяется, если известно аналитическое выражение выходного параметра через параметры деталей. Согласно выражению (4) для определения коэффициента влияния необходимо:
- взять частные производные выходного параметра по каждому из параметров деталей;
- умножить полученные частные производные на отношение параметра ![]() -го элемента к значению выходной характеристики;
-го элемента к значению выходной характеристики;
- подстановкой номинальных значений параметров деталей в выражение коэффициентов влияния найти их численные величины.
Выполнение перечисленных операций, особенно нахождение частных производных, связано с большим количеством промежуточных преобразований и требует значительных затрат времени. Поэтому этот метод, как правило, оказывается сложным и трудоемким даже при определении коэффициентов влияния параметров элементов на выходной параметр простейшего функционального узла как функции 6-10 переменных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.