Выявление закона распределения погрешностей и определение его числовых характеристик выполняется методами математической статистики.
Пусть исследуется величина Х – значение параметра радиоэлемента, которая в каждом конкретном случае принимает определённое значение. Если разделить весь диапазон наблюдаемых значений на интервалы (разряды), подсчитать количество значений mi, приходящихся на каждый i-й разряд, и это число разделить на общее число наблюдений n, то получим частоту, соответствующую данному разряду
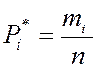 .
.
Сумма частот всех разрядов, очевидно, будет равна единице. Сводя
полученные значения ![]() в табл.1, получим статистический
ряд:
в табл.1, получим статистический
ряд:
Т а б л и ц а 1
|
Интервал |
|
|
. . . |
|
|
|
Частота |
|
|
. . . |
|
|
|
Вероятность |
|
|
. . . |
|
|
 Число разрядов желательно выбирать не меньше 10.
Число разрядов желательно выбирать не меньше 10.
Статистический ряд можно представить в виде гистограммы (рис. 1). На оси абсцисс откладываются интервалы, соответствующие разрядам, и на каждом из них, как на основании, строятся прямоугольники, высоты которых выбираются так, чтобы площади их равнялись частоте данного разряда (в случае равных по длине разрядов высоты прямоугольников будут пропорциональны соответствующим частотам).
При увеличении числа опытов и уменьшении длины интервалов (увеличении количества разрядов) гистограмма всё более будет приближаться к некоторой кривой, ограничивающей площадь, равную единице. Эта кривая представляет собой график плотности распределения случайной величины Х.
Каждой числовой характеристике непрерывной случайной величины соответствует её статистическая аналогия:
- математическому ожиданию – статистическое среднее (среднее арифметическое)
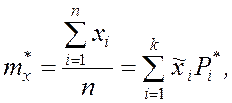
- дисперсии случайной величины – статистическая дисперсия
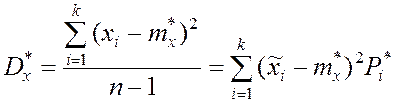 , где
, где ![]() – среднее значение случайной величины в i-м разряде;
– среднее значение случайной величины в i-м разряде; ![]() – частота i-го разряда; k – число
разрядов.
– частота i-го разряда; k – число
разрядов.
Любому статистическому распределению в большей или меньшей мере присущи элементы случайности. Для выявления его существенных черт оно выравнивается (сглаживается) путём подбора такой теоретической кривой распределения, которая наилучшим образом описывает данное статистическое распределение. Например, если исследуемая случайная величина Х – следствие большого числа независимых, примерно равных по своему влиянию случайных факторов, то из теоретических соображений можно считать, что она распределена по нормальному закону.
Когда вид теоретической функции подобран, её числовые характеристики
(обычно mx
и Dx)
выбираются так, чтобы они были равны соответствующим статистическим
характеристикам ![]() и
и ![]() . После
этого рассчитывается значение функции для середины каждого разряда. Этот метод
получил название метода моментов. В случае нормального закона плотность
распределения f(x) в i-й точке будет
. После
этого рассчитывается значение функции для середины каждого разряда. Этот метод
получил название метода моментов. В случае нормального закона плотность
распределения f(x) в i-й точке будет
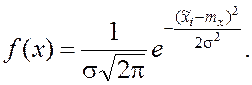
Результаты расчётов записываются в таблицу статистического ряда распределения. По найденным значениям на одном графике с гистограммой строится выравнивающая теоретическая кривая.
Соответствие кривой статистическому распределению оценивается одним из
критериев согласия. Наиболее распространённым является так называемый "критерий
c2 " Пирсона,
при котором согласованность между теоретическим статистическим распределениями
оценивается расхождением между вероятностями Pi попадания
случайной величины в каждый из разрядов и наблюдаемыми частотами ![]() . При нормальном законе теоретическая
вероятность попадания случайной величины в i-й разряд определяется
через функцию Лапласа
. При нормальном законе теоретическая
вероятность попадания случайной величины в i-й разряд определяется
через функцию Лапласа
|
|
|
|
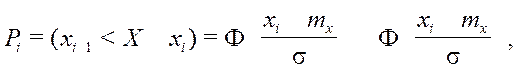
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.