3. Рассчитать допуски на частоту автоколебаний мультивибратора методами предельных отклонений и вероятностным. Допуски на параметры радиоэлементов задаются преподавателем.
4. Сравнить результаты расчета.
Содержание отчета
1. Цель работы.
2. Исходные формулы для расчета.
3. Блок-схема испытаний и результаты эксперимента.
4. Определение коэффициентов влияния методами расчетно-аналитическим и малых приращений.
5. Расчет допусков методами предельных отклонений и вероятностным.
6. Выводы.
1. Как составляется исходное уравнение для определения погрешностей?
2. В чем заключаются особенности расчета допусков методами предельных отклонений и вероятностным?
3. Когда применяются методы расчетно-аналитический и малых отклонений для определения коэффициентов влияния? Их особенности.
4. Что понимается под коэффициентом влияния?
5. В чем заключаются задачи анализа и синтеза допусков?
6. Какие существуют виды допусков?
7. Что понимается под коэффициентами относительного рассеивания и относительной асимметрии?
8. Как работает мультивибратор?
ОПРЕДЕЛЕНИЕ ТОЧНОСТИ
МЕТОДОМ МАТРИЧНЫХ ИСПЫТАНИЙ
Цель работы. Изучение метода матричных испытаний и экспериментальное определение работоспособности усилителя низкой частоты (УНЧ).
1. Матричные испытания УНЧ.
2. Определение вероятности работоспособного состояния УНЧ.
3. Оптимизация параметров УНЧ.
Методические указания
Метод матричных испытаний – метод физического моделирования. Он позволяет определить рабочую область радиоустройства при всех возможных значениях первичных параметров, находящихся в пределах допусков, оптимизировать его работоспособность.
Первичные параметры можно разбить на следующие группы:
- параметры деталей, из которых состоит устройство;
- параметры источников питания;
- параметры входных сигналов;
- параметры нагрузки;
- параметры, характеризующие условия окружающей среды.
Суть метода матричных испытаний и задачи оценки и оптимизации работоспособности по результатам этих испытаний поясним на примере устройства, работоспособность которого существенным образом зависит только от двух первичных параметров X1 и X2. Такие параметры будем называть определяющими первичными параметрами.
Пусть диапазон возможного изменения этих параметров задан интервалами [ x1 min , x1 max ] и [ x2 min , x2 max ]. Разобьем интервалы на l(1) и l(2) равных квантов соответственно (рис. 1).
В качестве представителей квантов выберем значения параметров, соответствующие серединам квантов. Если устройство оказывается неработоспособным (работоспособным) при значении параметров, соответствующем представителю кванта, то будем считать, что оно не работает (работает) при всех значениях параметров, лежащих в этом кванте.
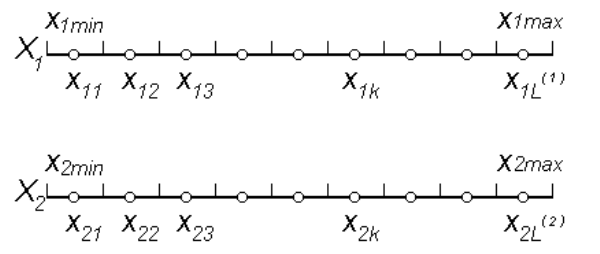
Рис. 1. Пример разбиения параметров X1 и X2 на кванты
Введем понятие ситуации, под которым будем понимать такое состояние устройства, когда каждый из его двух определяющих параметров (двумерный случай) принимает значение, соответствующее представителю определенного кванта. Определение легко распространить на n-мерный случай. Число всех возможных ситуаций устройства в двумерном случае, очевидно, равно
![]() .
.
Индекс 2 при N означает, что рассматривается двумерный случай, т.е. имеются два определяющих параметра. В общем случае при n определяющих параметрах число возможных ситуаций равно
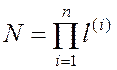 .
.
Перебрав в какой-либо последовательности все несовместные ситуации устройства, составим матрицу ситуаций. Для двумерного случая она будет иметь вид
![]()
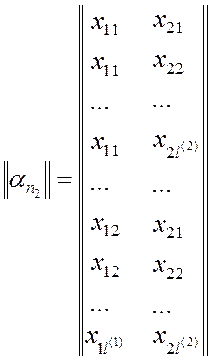
В матрице вторая строка x11 x22, например, означает, что параметр X1 принял значение в первом, а параметр X2 – во втором кванте.
Упорядоченную таким образом последовательность всех возможных ситуаций устройства обозначим
a1, a2, a3, ... , aN2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.