Под
начальными (первичными) параметрами ![]() и выходными параметрами
N в зависимости от
конкретной задачи могут пониматься размеры деталей, параметры
электрорадиоэлементов и т.д. Например, в формуле емкости между двумя
коаксиальными цилиндрами
и выходными параметрами
N в зависимости от
конкретной задачи могут пониматься размеры деталей, параметры
электрорадиоэлементов и т.д. Например, в формуле емкости между двумя
коаксиальными цилиндрами
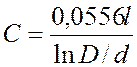 (2)
(2)
выходной
параметр С –
емкость, первичные параметры ![]() ,Dи
d –
соответственно
активная длина цилиндров, внутренний диаметр наружного цилиндра, наружный
диаметр внутреннего цилиндра.
,Dи
d –
соответственно
активная длина цилиндров, внутренний диаметр наружного цилиндра, наружный
диаметр внутреннего цилиндра.
Подставляя
в зависимость (1) по одному случайному значению ![]() , получим одно
случайное значение N.
Если многократно повторить расчет, подставляя каждый раз новые случайные
значения
, получим одно
случайное значение N.
Если многократно повторить расчет, подставляя каждый раз новые случайные
значения ![]() , выбранные в соответствии с их законами
распределения, то получим множество случайных значений N.
Обработав эти статистические данные, можем построить гистограмму и определить
закон распределения параметра N.
, выбранные в соответствии с их законами
распределения, то получим множество случайных значений N.
Обработав эти статистические данные, можем построить гистограмму и определить
закон распределения параметра N.
Часто
достаточно определить вероятность попадания параметра в пределы поля допуска,
т.е. ![]() . На основе теоремы Бернулли при достаточно
большом числе опытов за искомую вероятность можно принять частоту
(статистическую вероятность), определяемую по формуле
. На основе теоремы Бернулли при достаточно
большом числе опытов за искомую вероятность можно принять частоту
(статистическую вероятность), определяемую по формуле
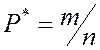 , где m–
число попаданий параметраNв
заданный интервал;
, где m–
число попаданий параметраNв
заданный интервал;
n – общее количество вычислений.
Ошибка
![]() в определении искомой вероятности P
по частоте
в определении искомой вероятности P
по частоте ![]() в зависимости от доверительной вероятности
в зависимости от доверительной вероятности ![]() и числа вычислений n
находится по формуле
и числа вычислений n
находится по формуле
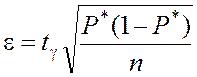 , где
, где
![]() – параметр распределения Стьюдента (берется
из табл. П3 приложения).
– параметр распределения Стьюдента (берется
из табл. П3 приложения).
Случайные
значения параметров ![]() могут моделироваться на ЭВМ.
Методы такого моделирования подробно описаны в учебном пособии [5] или
находятся при помощи таблиц случайных чисел [4], приведенных в табл.П4.- П7.
могут моделироваться на ЭВМ.
Методы такого моделирования подробно описаны в учебном пособии [5] или
находятся при помощи таблиц случайных чисел [4], приведенных в табл.П4.- П7.
Пояснения к таблицам случайных чисел
В табл. П4 приведены случайные числа, равномерно
распределенные в интервале от 0 до 10000. Для того чтобы получить отсюда
случайные числа ![]() , равномерно распределенные в
интервале от 0 до 1, нужно все числа разделить на 10000.
, равномерно распределенные в
интервале от 0 до 1, нужно все числа разделить на 10000.
Если
нужны случайные числа ![]() , равномерно распределенные в интервале
от a,
до b,
тоих можно получить при помощи линейного преобразования
, равномерно распределенные в интервале
от a,
до b,
тоих можно получить при помощи линейного преобразования
![]() .
(3)
.
(3)
Пример. Найти три случайных числа, равномерно распределенных в интервале от 20 до 120.
Решение. Используя первые три числа из табл. П4 и уравнение (3), в котором полагаем a = 20, b= 120, получаем:
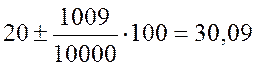 ;
;
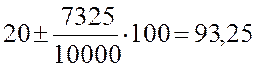 ;
;
![]() .
.
В табл. П5 показаны случайныечисла ![]() длянормального распределения с
параметрами
длянормального распределения с
параметрами![]() =0и
=0и ![]() =10000.
=10000.
Если
нужны случайные числа ![]() ,
нормально распределенные с параметрами
,
нормально распределенные с параметрами ![]() , тоих можно получить при помощи линейного преобразования
, тоих можно получить при помощи линейного преобразования
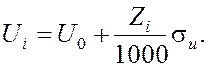 (4)
(4)
Пример.
Найти два случайных числа для нормального распределения с параметрами ![]() = 1000,
= 1000,
![]() = 200.
= 200.
Решение. Используя первые два числа из табл. П5, находим при помощи уравнения (4):
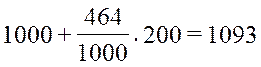 ;
;
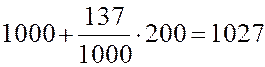 .
.
В
табл. П6 помещены случайные числа ![]() , отвечающие экспоненциальному
распределению с математическим ожиданием 1000. Если нужны случайные числа с
математическим ожиданием
, отвечающие экспоненциальному
распределению с математическим ожиданием 1000. Если нужны случайные числа с
математическим ожиданием ![]() , тоих можно
получить при помощи линейного преобразования
, тоих можно
получить при помощи линейного преобразования
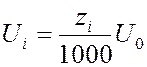 .
(5)
.
(5)
Пример. Найти два случайных числа, отвечающих экспоненциальному распределению с математическим ожиданием U0 = 500.
Решение. Используя первые два числа из табл. П6, находим при помощи уравнения (5):
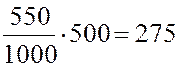 ;
;![]()
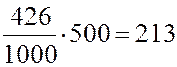 .
.
В табл. П7 приведены случайные числа ![]() , отвечающие распределению Вейбулла
с параметрами b= 1,5 и математическим ожиданием 1000.
Если нужны случайные числа
, отвечающие распределению Вейбулла
с параметрами b= 1,5 и математическим ожиданием 1000.
Если нужны случайные числа![]() , отвечающие распределению Вейбулла с математическим
ожиданием
, отвечающие распределению Вейбулла с математическим
ожиданием![]() , то их можно получить
при помощи линейного преобразования
, то их можно получить
при помощи линейного преобразования
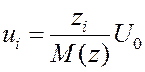 .
(6)
.
(6)
Пример.
Найти два случайных числа, отвечающих распределению Вейбулла с параметрами b=
1,5 и ![]() =
100.
=
100.
Решение. Используя два первых числа из табл. П7, для b= 1,5 находим при помощи уравнения (6):
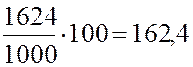 ;
;
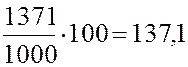 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.