
































Кафедра БДУиА
КОНСПЕКТЫ ЛЕКЦИЙ
по дисциплине «ММ экономических систем»
для студентов 4 курса спец. 060500, 060800, 061100
и направлению подготовки 521600
Составитель:
кт.н., доц. С.Н.Мельгунова
Введение
Методология исследования операций (ИО) формировалась на протяжении последних десятилетий под влиянием интенсивных разработок в различных сферах человеческой деятельности: экономико-организационных, космических, энергетических, оборонных систем и способов их практического использования. Важным этапом этого процесса явилось изучение информационных аспектов деятельности человека, что способствовало развитию идей автоматизированного управления.
Проектирование и эксплуатация автоматизированных систем представляют собой последовательную цепь операций. Цель любого проектирования – создание системы, отвечающей замыслу и требованиям технического задания, имеющей хорошие технико-экономические показатели, удобной в эксплуатации и обслуживании.
Исследование операций базируется на следующих понятиях: операция; оперирующая сторона; лицо, принимающее решение; стратегия; действующие факторы: критерии эффективности; математическая модель; математическое программирование.
На базе приведенных понятий формулируется основная задача исследования операций – найти в рамках принятой модели такие решения, которые соответствуют экстремальным значениям критерия эффективности операции.
В каждой лабораторной работе приводятся необходимые теоретические сведения, расчетные соотношения, методика выполнения задания и примеры, а также варианты заданий.
Лекция № 1
Многокритериальные задачи ИО. Преодоление неопределенности целей
Цель работы – исследование методов преодоления неопределенности целей в многокритериальных задачах ИО.
Теоретические сведения
На практике задачи ИО, где критерии оценки однозначно определяются целевой направленностью операции, встречаются редко. В большинстве случаев операция представляет собой задачу крупного масштаба, затрагивающую разнообразные интересы участников, и характеризуется различными показателями эффективности. Такие задачи ИО называются неопределенными. При их рассмотрении говорят о неопределенности целей. Преодоление неопределенности осуществляется следующими способами.
1. Линейная свертка.
Вместо n – частных критериев wi предлагается рассматривать один критерий вида
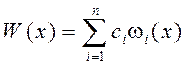 ,
(1.1)
,
(1.1)
где 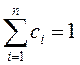 –
коэффициенты, определяемые методом экспертных оценок.
–
коэффициенты, определяемые методом экспертных оценок.
Коэффициенты ciотражают представление оперирующей стороны о содержании компромисса, который она вынуждена принять. Таким образом, содержание компромисса заключается в ранжировании целей.
2. Использование контрольных показателей.
Часто в задачах планирования и проектирования задается
некоторая система нормативов w1*,ω2*,
… ωi*, …, ωn*. Это значит, что параметр будущего решения должен быть таким, чтобы
максимизировать функции ωi(x) при условии ![]() . В этом случае целевая функция может быть
представлена в виде
. В этом случае целевая функция может быть
представлена в виде
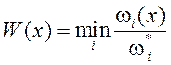 .
(1.2)
.
(1.2)
Здесь необходимо искать вектор x,который обеспечивает максимальное значение W(x).
Если значения ![]() жестко не заданы, то их
определяют в результате экспресс-опроса. Эти задачи могут быть сведены к задаче
линейного программирования следующим образом:
жестко не заданы, то их
определяют в результате экспресс-опроса. Эти задачи могут быть сведены к задаче
линейного программирования следующим образом:
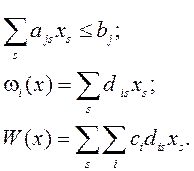
Введем новую переменную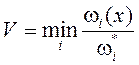 . Тогда решение задачи состоит в нахождении
решений, которые удовлетворяют следующим условиям
. Тогда решение задачи состоит в нахождении
решений, которые удовлетворяют следующим условиям ![]() .
.
3. Простейший способ преодоления неопределенностей.
Пусть опять введена некоторая система контрольных
показателей![]() , относительно которых
критерии
, относительно которых
критерии ![]() удовлетворяют ограничениям
удовлетворяют ограничениям
![]() .
.
Если возможно выбрать основной (главный) критерий, то
приходим к однокритериальной задаче ![]()
4. Введение метрики в пространстве целевых функций.
Предположим, что решена система однокритериальных
задач ![]() и
решение задачи представляет собой вектор
и
решение задачи представляет собой вектор![]() , доставляющий экстремальное значение
критерию
, доставляющий экстремальное значение
критерию![]() , т. е.
, т. е.
![]() .
.
Совокупность скалярных величин ![]() определяет в пространстве
критериев некоторую точку – «точку абсолютного экстремума».
определяет в пространстве
критериев некоторую точку – «точку абсолютного экстремума».
Если векторы xi различны, то не существует такого выбора,
который позволил бы достичь этой точки. Таким образом, точка (![]() ,
,![]() ,…,
,…,![]() ) является точкой недостижимого абсолютного
экстремума в пространстве критериев. Введем положительно определенную матрицу
) является точкой недостижимого абсолютного
экстремума в пространстве критериев. Введем положительно определенную матрицу ![]() . Тогда метрическое
расстояние в пространстве целевых функций определяется выражением
. Тогда метрическое
расстояние в пространстве целевых функций определяется выражением
![]() . (1.3)
. (1.3)
При p= 1 – абсолютное расстояние, критерий (1.3) сводится к следующему:
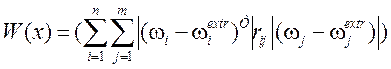 ,
(1.4)
,
(1.4)
а при р = 2 – евклидово расстояние
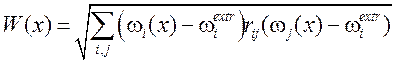 .
(1.5)
.
(1.5)
Скалярные величины (1.4), (1.5) определяют в пространстве критериев некоторое расстояние от точки, соответствующей данному вектору x, до точки «абсолютного экстремума».
Если![]() , где I – единичная матрица, то соотношения (1.4),
(1.5) преобразуются в следующие:
, где I – единичная матрица, то соотношения (1.4),
(1.5) преобразуются в следующие:
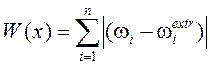 ,
(1.6)
,
(1.6)
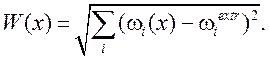 (1.7)
(1.7)
Лекция № 2
Компромиссы Парето. Численные методы
построения множества Парето
Цель работы – применение компромиссов Парето для преодоления неопределенности целей.
Теоретические сведения
При решении многокритериальных задач можно попытаться сократить множество исходных вариантов, т. е. исключить из рассмотрения те варианты решений, которые заведомо плохи (Парето, 1904).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.