ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 5

Следующая критическая работа а₈, для которой , что дает критическую работу а₆ и т. д. Продолжая, аналогично получим а₄, а₁. Итак, имеем критические работы а₁, а₄, а₆, а₈, а₁₀, которые составляют критический путь. Полученный результат совпадает с результатом критического пути, представленного на рисунке. Аналогично формально можно найти некритические дуги, а также резервы времени.

Лекция № 5

Системы массового обслуживания. Уравнения Колмогорова

Цель работы – изучить способы описания процессов и характеристик систем массового обслуживания.

Теоретические сведения

Примерами систем массового обслуживания (СМО) могут служить телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, парикмахерские и другие предприятия, занимающиеся обслуживанием массовых потоков клиентов или их требований.

СМО состоит из какого-то числа обслуживающих единиц – каналов (число линий связи, число телефонисток, число продавцов и т. д.). СМО могут быть одноканальные и многоканальные.

Работа СМО – это выполнение поступающего на нее потока заявок (потока требований), которые идут одна за другой в случайные моменты времени. Канал обслуживает заявку какое-то время (тоже в общем случайное) и освобождается. Каждая СМО обладает некоторой пропускной способностью, позволяющей ей относительно эффективно справляться с потоком заявок.

Для описания структуры и работы СМО необходимо определить:

·  n – число каналов СМО;

·  p_i – вероятность того, что в СМО занято обслуживанием ровно i каналов, например, p₀ – все каналы свободны; p_n – занято n каналов;

·  – среднее число заявок, поступающих в СМО в единицу времени.

СМО делятся на два основных класса: СМО с отказами и СМО с ожиданием (очередностью). В СМО с отказами заявка, заставшая все каналы занятыми, получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует. В СМО с ожиданием заявка становится в очередь. В зависимости от организации очереди могут быть ограниченные или неограниченные, очередь с ограниченным временем ожидания и т. п. Для классификации СМО важное значение имеет дисциплина обслуживания (правила обслуживания) заявок: первая пришла – первая обслужена (FIFO), последняя пришла – первая обслужена (LIFO), обслуживание с приоритетом и т. п.

Наиболее употребительными показателями эффективности функционирования СМО являются следующие:

·  вероятность отказа в обслуживании p_от, которая для СМО с отказами будет p_от = p_n;

·  среднее число занятых каналов или среднее число заявок, находящихся в обслуживании 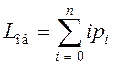, характеризующее степень загрузки обслуживающей системы;

·  среднее число свободных, простаивающих от обслуживания каналов

;

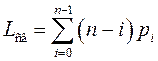·  коэффициент простоя канала ;

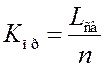·  коэффициент занятости канала ;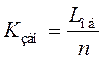

·  для СМО с отказами вводится понятие относительной Qи абсолютной Aпропускной способности системы

Q = 1 – P_отк,  A=Q.

Для СМО с ожиданием вводятся следующие понятия: L_сист – среднее число заявок в очереди; Т_сист –  среднее время пребывания заявки в системе; Т_оч  –  среднее время пребывания заявки в очереди.

Процесс функционирования любой СМО представляет собой случайный процесс. СМО присущ тип случайного процесса с дискретным состоянием, когда возможные состояния, характеризующие систему S₀, S₁, S₂,…, можно перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком) в любой момент времени (процесс с непрерывным временем). Такой процесс следует отнести к случайному процессу, квантованному (дискретизированному) по уровню.

При анализе такого рода процессов удобно пользоваться графической системой – графом состояния. Состояния системы будут являться вершинами графа, а возможные переходы из состояния в состояние – ребрами. Математический анализ СМО значительно упрощается, если процесс работы СМО – марковский, а поток заявок (поток событий) – простейший.

Случайный процесс называется марковским или случайным процессом без последействия, если для любого времени t₀ вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент времени t₀ и не зависят от того, как система пришла в это состояние (от предыстории).