ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 2

Предположим, что сделан некоторый выбор x^*. И пусть существует другой выбор x⁰ такой, что для всех критериев  имеет место неравенство

, причем хотя бы одно неравенство строгое. Тогда все x^* нужно исключить из рассмотрения. Подвергать анализу следует только те x^*, для которых не существует x⁰, удовлетворяющих неравенству. Множество всех таких значений называют множеством Парето, а вектор x^*– неулучшаемым вектором результатов (вектором Парето), если из неравенства  для любого i следует.

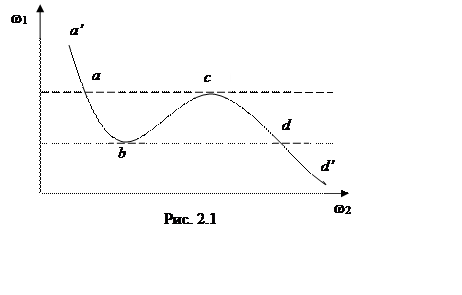
Пример 1. Пусть цели линейного программирования определяются двумя критериями ;  (рис. 2.1). Тогда каждому допустимому значению переменной x отвечает одна точка на плоскости . Участок [a, c[ не принадлежит к множеству Парето, поскольку доминируется отрезком [c, d].

Рис.1

Следо-вательно, к множеству Парето принадлежат участки [a’, a] и [c,d’].

В теории принятия решения существует «принцип Парето» – выбирать в качестве решений следует только те, которые принадлежат к множеству Парето. Принцип Парето не выделяет единственное решение – он сужает лишь множество альтернатив.

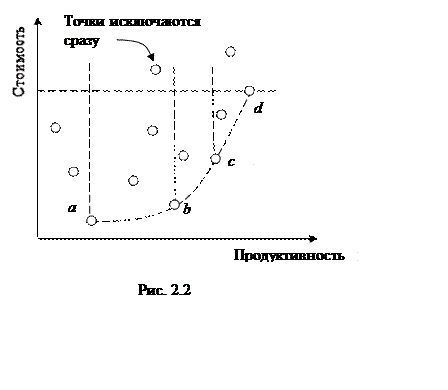
Пример 2. Пусть предстоит сделать выбор между некоторыми вариантами решений (x₁, x₂, …,x_n) (рис. 2.2). Эффективность операции оценивается показателями «продуктивность – стоимость», причем первый стремится к максимуму, а второй – к минимуму.

Из множества Парето следует исключить все точки, кроме точек, связанных пунктирами a – b – c – d. Поскольку для всех других вариантов найдется такой из точек a – b – c – d, для которого продуктивность выше при меньшей стоимости и наоборот.

Рис.2

Построение множества Парето относится к числу очень важных и трудных задач численного анализа.

Пусть требуется найти множество Парето для следующего случая, ,  .

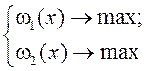Каждой точке  соотношения  ставят в соответствие точку  в плоскости критериев (рис. 2.3).

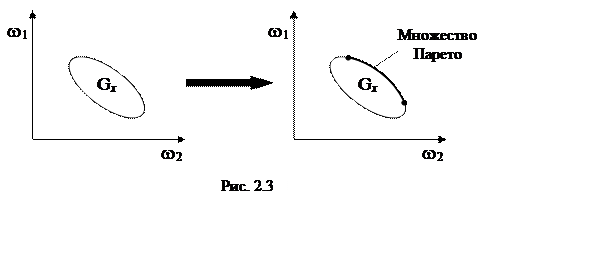
Множество  – множество достижимости, или множество предельных возможностей. Приближенное построение множества Парето сводится к последовательному решению ряда задач математического программирования.

Примерный план построения множества Парето.

1. Фиксируются некоторые желательные значения критериев ω₁ и ω₂, т. е.; , где.

2. Решаем две оптимизационные задачи:

а)                                        б)

                               

Решив эти задачи, определяем точки a и b.

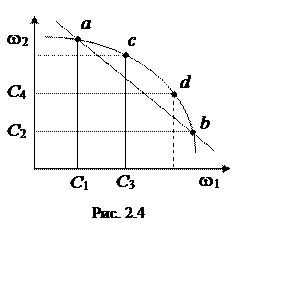Проведя через них прямую, получим простейшую аппроксимацию множества Парето.

3. Для уточнения множества решают еще две оптимизационные задачи:

а),      б),  Решив задачи а и б, получаем точки c и d – таким образом, множество Парето уточняется.

Лабораторная работа № 3

Детерминированные модели операций. Линейное и нелинейное программирование

Цель работы – изучить методику решения оптимизационных задач с линейной и квадратичной целевыми функциями.

Теоретические сведения

В наиболее общей форме задачу оптимизации можно сформулировать следующим образом: найти экстремум (максимум или минимум) функции

y = f(x) = f(x₁, …,x_n), xÎD,(3.1)

где y – скалярная величина; x = col[x₁, …, x_n], D – некоторая область в n-мерном пространстве. Функцию y = f(x) называют целевой, так как ее максимизация (минимизация) часто есть формальное выражение какой-то цели (например, найти максимум прибыли или минимум затрат и т. п.). Решением задачи оптимизации является вектор входных (управляющих) переменных x_i, при которых выходной вектор y будет максимальным (минимальным). Если область D совпадает со всей областью определения функции f(x), то имеем постановку задачи поиска безусловного экстремума, если же D только часть области определения, то имеем задачу на условный экстремум.

В задаче на условный экстремум область D обычно определяет некоторые ограничения на переменные x_i, которые следуют из физических соображений и которые учитывают внутренние и внешние условия функционирования системы.

В наиболее полной форме область D может быть задана в виде системы равенств или неравенств:

φ₁(x₁, …,x_n){≤,=,≥,}b₁,