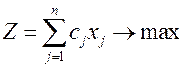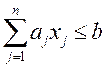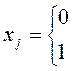ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 9

,   ,    , .

К такой постановке приводит также задача распределения капиталовложений: имеется n проектов использования капиталовложений, объем которых равен b. Для каждого проекта известны расходы a_j и прибыль c_j от его реализации. Проекты независимы друг от друга. При этом наличных ресурсов недостаточно для осуществления всех проектов. Требуется определить набор проектов, обеспечивающих в пределах ресурсов максимальную прибыль.

Задача данного типа может быть расширена за счет нескольких ограничений:

.

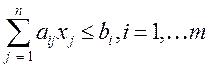«Задача о коммивояжере». Бродячий торговец должен покинуть город 1 и объехать еще N–1 городов, затем опять вернуться в город 1. В его распоряжении есть дороги, соединяющие города. Он должен выбрать маршрут, порядок посещения городов так, чтобы путь был как можно короче. Условие – коммивояжер не имеет права возвращаться снова в тот город, в котором побывал. Длина пути определяется формулой 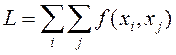, где  – расстояние между городами (в общем случае ).

Решение целочисленной задачи линейного программирования отличается от решения задач линейного программирования наличием дополнительного условия целочисленности. Рассмотрим простой пример.

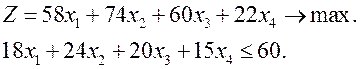
Без условия целочисленности получаем , . При наличии условия целочисленности (– целое, ) получаем , .

Решение целочисленных задач осуществляется методами отсечения и комбинаторики.

Метод отсечения состоит в последовательном отбрасывании некоторых подмножеств области, которые не содержат целых точек.

Метод комбинаторики – метод анализа дискретных множеств, основанных на выделении и упорядочении последовательностей (выборок, комбинаций) подмножеств. Их общая идея – замена полного перебора всех подмножеств частичными переборами. Одним из эффективных методов является метод ветвей и границ.

Данный метод рассматривает основную задачу как последовательность подзадач на непересекающихся подмножествах P₁, P₂, …, P_n, таких, что ,  при i ≠ j.

Совокупность определенных таким образом подмножеств называется разбиением подмножества Р, процесс построения подмно-жеств – ветвлением, а задачи (подзадачи) – задачами-кандидатами.

Задачи-кандидаты (ЗК) состоят в ослаблении (релаксации) некоторых условий исходной задачи без изменения ее целевой функции. В результате вместо ЗК с допустимой областью P_j получаем ее релаксацию, т. е. ЗКР.

Решение вспомогательной задачи дает верхнюю границу целевой функции на подмножестве. Если при этом оказывается, что элемент, на котором достигается верхняя граница целевой функции, принадлежит P_j, то он называется решением-претендентом, а значение целевой функции – рекордом. Если затем в процессе ветвления находится элемент с большим значением целевой функции, то он становится новым планом-претендентом, а целевая функция – новым рекордом.

Процесс решения заканчивается, когда имеется некоторое разбиение {P_i} I =1,…,rи план претендент  такой, что,  ,  i ≠ k.

В соответствии с этим найденный план считается оптимальным. Процесс выполнения подмножеств может быть представлен в виде дерева – специального графа, все вершины которого имеют единственную входную дугу (рис. 8.1).

Рис. 8.1

Каждая вновь полученная в процессе ветвления ЗК отличается от входящей в список задач-кандидатов. Она находится в нем, пока не будет прозондирована, т. е. удалена из списка как неперспективная или разветвлена – заменена в списке новыми подзадачами.

ЗК считается прозондированной, если в результате решения ЗКР выполнен один из критериев.

1. ЗКР не имеет допустимого решения. В таком случае следует исключить ЗК из дальнейшего рассмотрения, т. к. она так же недопустима.

2. Оптимальное значение целевой функции ЗКР меньше или равно текущему рекорду. В этом случае ни на одном из допустимых решений ЗК не может достигнуть значения целевой функции большее, чем имеющийся рекорд, следовательно, решение исключается из дальнейшего рассмотрения.

3. Оптимальное значение (решение) ЗКР целочисленно. В этом случае дальнейшее ветвление ЗК не даст целочисленного решения с большим значением целевой функции. Полученное решение становится решением-претендентом, а целевая функция – новым рекордом. В противном случае решение претендент и верхняя граница остаются прежними. В обоих случаях ЗК исключается из списка.