ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 11

Определим ход решения (нахождение оптимальной стратегии) для участников А и В. Для А наилучшая стратегия обуславливается достижимым, гарантированным результатом, т. е. пусть А выбирает стратегию поведения S_iА максимизирующую ее выигрыш, тогда сторона В дает для А  . Таким образом, стратегия для А, обеспечивающая гарантированный результат, – максиминная стратегия:  Величина a называется нижней ценой игры или максиминным выигрышем. Для В ситуация противоположная, сторона В должна обеспечить максимальный проигрыш А. Поскольку ПВ = – ПА = – а, то   Величина b – минимаксный проигрыш, верхняя цена игры. Поскольку модель дуальна (симметрична), то используется общепринятое название «минимаксная стратегия».

Каждая из сторон ориентирована на худшую с ее точки зрения ситуацию. Простейшим, но редко встречающимся случаем является случай  – это равенство означает, что в игровой матрице присутствует элемент a_pq, который одновременно оказывается минимальным в p – строке и максимальным q-столбце (седловая точка) – их может быть несколько. Такая ситуация  называется ситуацией  равновесия,  т. е. положением, при котором ни одна из сторон не изменяет своей стратегии. Величина a_pq называется чистой ценой игры, а стратегии – чистыми стратегиями. Применять чистые стратегии имеет смысл только тогда, когда А и В располагают сведениями друг о друге. Отсюда различие – игры с полной информацией и игры с неполной информацией. Для практических задач распространенным является случай. Кроме этого, в условиях непредсказуемости хода противника каждому выбору определенной стратегии S_ix соответствует некоторая p_ix, причем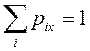. Произвольно взятое распределение  называется смешанной стратегией. При выборе стратегий поведения сторон пользуются усреднением, т. е. принцип минимакса сохраняется и в этом случае:

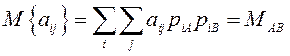,                              (9.2)

                             (9.3)

                             (9.4)

Теорема об активных стратегиях говорит, что если один из участников игры придерживается своей оптимальной стратегии, то ожидаемый выигрыш остается неизменным и равным  независимо от характера действий другого участника в пределах его активных стратегий.

Рассмотрим пример антагонистической игры (2‰2) с заданными коэффициентами а_ij, и пусть игра не имеет седловой точки. Требуется найти решение, т. е определить .

Согласно теореме об активных стратегиях неизвестные значения  могут быть получены из следующих соотно-шений:

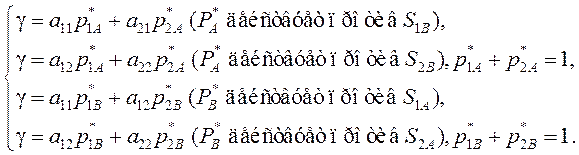  (9.5)

Рассмотрим более общий случай игры . При этом применима стратегия  против какой либо  и стратегия  против . Тогда справедливы формулы

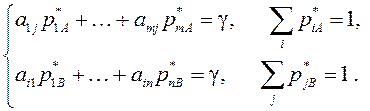                   (9.6)

Введем в рассмотрение функции

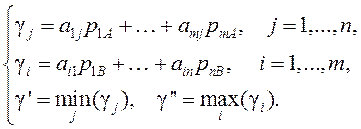                  (9.7)

Тогда получаем

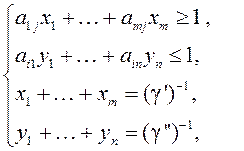                            (9.8)

где обозначено

Стремление стороны А максимизировать свой выигрыш  равносильно требованию минимизации . Вторая сторона конфликта В преследует противоположную цель – достичь максимума , т. е. минимизировать . Задачу (9.8) можно решить с помощью линейного программирования. Постановка задачи линейного программирования в этом случае выглядит так:

·  найти 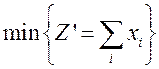, при ограничениях  ,

·  найти 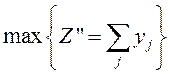, при ограничениях   .

Литература

1. Дегтярев Ю. И. Исследование операций. – М.: Высш. шк., 1986. – 320 с.

2. Волков И. К., Загоруйко Е. А. Исследование операций: Учебник для вузов / Под ред. В. С. Зарубина,  А. П. Крищенко. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2000. – 436 с. (Сер. Математика в техническом университете, Вып. ХХ).

3. Исследование  операций:   В  2-х т.;  Под.  ред.  Дж.  Моудера,  С. Элмаграби. – М.: Мир,1981. – Т. 1. – 712 с.

4. Кини Р. Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения / Под. ред. И. Ф. Шахнова. – М.: Радио и связь,1981. – 560 с.

5. Матвеев Л. А. Компьютерная поддержка решений: Учебник. – СПб.: Специальная литература, 1998. – 472 с.

6. Мину М. Математическое программирование. Теория и алгоритмы. – М.: Наука, 1990. – 488 с.

7. Подиновский В. В., Ногин В. Д. Парето – оптимальные решения многокритериальных задач. – М.: Наука, 1982. – 256 с.