ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 3

…………………………                                                            (3.2)

φ_m(x₁, …,x_n) {≤,=,≥,}b_m.

В случае задачи условной оптимизации ее решением является вектор входных переменных x_i, удовлетворяющий ограничениям (3.2) и доставляющий скаляру y максимальное (минимальное) значение. Следует отметить, что при решении такого типа задач, помимо нахождения экстремумов целевой функции, удовлетворяющих условиям (3.2), необходимо исследовать поведение целевой функции на границах области ограничений (3.2), т. к. значения функции y на границах исследуемой области могут оказаться больше (в случае максимума) или меньше (в случае минимума) полученных экстремальных значений целевой функции. Именно это значение вектора x и следует считать решением задачи условной оптимизации.

Наиболее простой является задача линейного программирования: найти экстремум (максимум или минимум) функции

y = f(x) = c₁x₁ +…+ c_nx_n                                              (3.3)

при ограничениях (условиях)

a₁₁x₁ +…+ a_1nx_n{≤,=,≥} b₁,

………………………………                  (3.4)

a_m1x₁ +…+ a_mnx_n{≤,=,≥} b_m.

Наряду с условиями (3.4)  часто  требуют  выполнения условия x_i ≥ 0. Возможны  и прямые ограничения вида x_min £ x £x_max.

Более сложной задачей является задача нелинейного программирования, когда нелинейности содержит целевая функция (3.1) и (или) система ограничений (3.2). В зависимости от типа нелинейностей применяются различные численные методы решения данных задач. Использование аналитических методов затруднительно.

Задача квадратичного программирования является частным случаем задач нелинейного программирования, когда целевая функция имеет вид

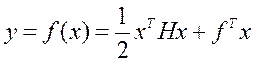,                         (3.5)

где матрица H и вектор f содержат коэффициенты при членах первого и второго порядка квадратичного полинома, а ограничения являются линейными (3.4).

Лекция № 4

Динамическое программирование

Цель работы – исследовать методы динамического программирования для решения задач оптимизации с использованием универсальных математических программных пакетов.

Теоретические сведения

Динамическое программирование представляет собой метод оптимизации многошаговых процессов принятия решения. Необходимость принятия решений возникает тогда, когда производятся те или иные целенаправленные действия (например, некоторая система переводится из одного состояния в другое посредством приложения управляющих воздействий). Следует отметить, что ход таких процессов не определен, его нужно организовывать, при чем так, чтобы получить наибольший эффект с точки зрения принятого критерия. Формально это означает минимизацию (или максимизацию) величины принятого критерия.

Динамическое программирование основывается на двух важных принципах: оптимальности и вложения. Принцип оптимальности состоит в необходимости всегда обеспечивать оптимальное (в смысле принятого критерия) продолжение процесса относительно уже достигнутого состояния. Это значит, что решение на каждом последующем шаге должно приниматься с учетом результата, полученного на всех предыдущих шагах.

Принцип вложения утверждает, что природа задачи не изменяется при изменении количества шагов. Другими словами, всякий конкретный процесс может оказываться вложенным в семейство подобных ему. Динамическое программирование может применяться для решения задач маршрутизации перевозок и выбора наикратчайшего пути, сетевого планирования комплекса работ и выбора наименьшего времени его выполнения и т. д.

Рассмотрим более подробно методику планирования комплекса работ. Пусть задан комплекс из 10 работ, представленных структурной временной табл. 4.1.

Таблица 4.1

Структурная временная таблица комплекса работ