В этом типе систем заявка, пришедшая в систему и застав все каналы занятыми, не покидает ее, а становится в очередь и ждет до тех пор, пока ее не обслужат. На время ожидания или длину очереди никаких ограничений не устанавливается.
Рассмотрим одноканальную систему с неограниченной очередностью. Система может находиться в следующих состояниях: S0 – канал свободен; S1– канал занят, очереди нет; S2 – канал занят, одна заявка стоит в очереди; S3 – канал занят, две заявки стоят в очереди и т. д. Граф состояний СМО приведен на рис. 7.1.
Рис. 7.1
Применяя правило составления уравнений Колмогорова для установившегося режима, будем иметь
μp1 – p0λ = 0, λpk–1 + μpk+1 – pk(μ+λ) = 0, k = 1, 2, … .
К этим уравнениям следует добавить нормировочное условие
p0 + p1 +…+ pk+…= 1.
Из первых двух уравнений нетрудно найти
, 
,… .
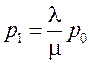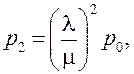
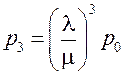Обозначим λ / μ = ρ, тогда p0(1 + ρ + ρ2 + ρ3 +…) = 1.
Уравнения для определения piприобретают вид
p0 = (1+ρ+ ρ2+ ρ3+…)–1,pk = ρk(1+ ρ+ ρ2+ ρ3+…)–1, k = 1, 2, … .(7.1)
В теории
доказано, что если ρ<1, то установившийся режим всегда
существует, бесконечная геометрическая прогрессия сходится (1+ρ+ ρ2+
ρ3+…) =
, и тогда окончательно получим
p0=1 – ρ, pk = ρk(1 – ρ). (7.2)
При ρ ≥ 1 очередь растет до бесконечности и установившегося режима не существует.
Среднее число
заявок в системе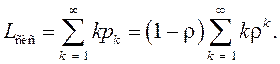 
Эта формула при ρ < 1 преобразуется к виду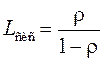
.
Среднее число заявок, находящихся в обслуживании, определим по формуле математического ожидания числа заявок в обслуживании, принимающей значение 0 (если канал свободен) либо 1 (если канал занят):
.
(7.3)
Найдем среднее число заявок в очереди Lоч. Очевидно, что
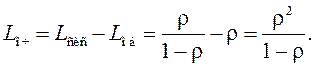(7.4)
Доказано, что при любых характере потока заявок, распределении времени обслуживания, дисциплине обслуживания среднее время пребывания заявок в системе (очереди) равно среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т. е.
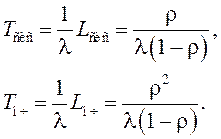(7.5)
Эти формулы называются формулами Литтла.
Рассмотрим n-канальную СМО с неограниченной очередью. Система может находиться в следующих состояниях: S0, S1, …,Sn, Sn+1,…, где S0 – все каналы свободны; S1– занят один канал и т. д., Sn+1 – заняты N каналов и одна заявка в очереди и т. д. Граф состояний системы приведен на рис. 7.2.
Рис. 7.2
При ρ ∕ n < 1 предельные вероятности существуют. Если ρ ∕ n ≥ 1, очередь растет до бесконечности. Формулы для вычисления вероятностей состояний имеют вид
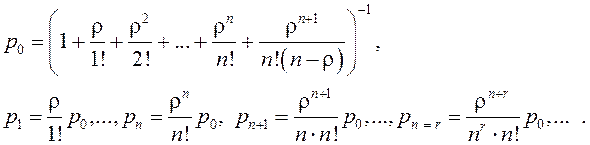(7.6)
Вероятность
того, что заявка окажется в очереди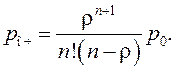 
Для N-канальной СМО можно найти
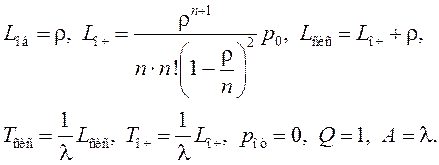(7.7)
Все приведенные формулы верны только при ρ < 1.
Лекция № 8
Дискретное и целочисленное программирование
Цель работы – изучить методы решения задач целочисленного программирования.
Теоретические сведения
К задачам дискретного программирования (ДП) относятся
задачи математического программирования, в которых требуется найти максимум
целевой функции, определяемой на некотором дискретном множестве 
.
Для решения задачи надо определить такой элемент 
, что 
.
Частным случаем является задача линейного
целочисленного программирования, которая формулируется как задача линейного
программирования, дополненная требованиями целочисленности всех или некоторых
переменных: 
; 
; 
– целое.
Если множество индексов j включает все j = 1,…,n, то задача называется полностью целочисленной. Если требования целочисленного программирования распространяются не на все элементы j = 1,…,n, то – частично целочисленной задачей линейного программирования.
К моделям дискретного программирования приводят задачи календарного планирования (теория расписаний), маршрутизация перевозок, синхронизация конвейера и т. д. Часто задачи ДП рассматриваются как «задачи о рюкзаке» или «задачи о коммивояжере».
«Задача о рюкзаке». Пусть дано n неделимых предметов, для каждого из которых известны стоимость cjи масса aj, j = 1…n. Рюкзак вмещает не более чем b единиц груза. С учетом вместимости рюкзака требуется составить набор
предметов максимальной ценности. Если ввести переменные 
(если j-тый
предмет входит в набор) и 
(если нет) получаем модель
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.