ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 4

Следует отметить, что все работы а_i  в таблице ранжированы, т. е. расположены в порядке их выполнения. Данная таблица является основой построения временного сетевого графика (рисунок), где A_i (вершины графа), – события, а a_i (ребра графа) – работы. Работы, представленные сплошными линиями, – фактические работы, характеризующиеся затратами времени, трудовых и материальных ресурсов, а пунктирными – фиктивные работы, показывающие резервы времени (ожидание). Очевидно, событие A₁₀ = A– окончание всего комплекса работ.

Последовательность работ в сети, в которой конечное событие каждой работы совпадает с начальным событием следующей, называется путем. Например, путь A₀–a₂–A₂–A₃–a₅–A₅ – это путь от события А₀ к событию А₅. Критическим путем назовем путь от события А₀ до события А, который не имеет в своем составе фиктивных работ. Он определяет минимальное время Т, за которое может быть совершен комплекс работ. Из рисунка видно, что критический путь – это путь А₀–а₁–А₁–а₄–А₄–а₆–А₆–а₈–А₈–а₁₀–А. Работы, лежащие на критическом пути, носят название критических работ. Очевидно, что время T = t₁ + +t₄ + t₆ + t₈ + t₁₀ = 10 + 18 + 18 + 25 + 8 = 79.

Заметим, что в общем случае на сетевом графике может быть несколько критических путей. Все остальные пути из А₀ в А являются некритическими и имеют суммарное время выполнения работ меньше 79, т. к. содержат фиктивные работы.

Рисунок

Критический путь на сетевом графике – это совокупность наиболее уязвимых работ плана, которые должны выполняться четко во времени.

Любое затягивание критических работ будет увеличивать минимальное время Т выполнения всего комплекса работ. Что касается остальных «некритических» работ комплекса а₂, а₃, а₅, а₈, а₁₀, то они все имеют резервы времени и их выполнение может быть при желании затянуто.

Знание критического пути позволяет выделить и контролировать наиболее важные работы, а знание резервов времени по некритическим работам – маневрировать материальными и людскими ресурсами, перебрасывая их с некритических работ (соответственно затягивая их выполнение) на критические (ускоряя их выполнение). Это позволяет уменьшать время Т выполнения всего комплекса работ.

Графический способ описания задачи сетевого планирования и анализ сетевого графика пригодны лишь для случая, когда количество работ, входящих в комплекс, невелико.

Существующие задачи иногда включают сотни и тысячи работ, взаимосвязанных между собой сложным образом, и составление сетевого графика, а тем более анализ его ручными способами практически невозможен. Поэтому разработаны алгоритмы составления и анализа сетевых графиков на базе аналитических моделей, которые можно положить в основу программных средств анализа.

Обозначим  – минимальное время начала работы а_i (время отсчитываем от начала сети), а Т_i – минимально возможный срок ее окончания. Время выполнения работы обозначим t_i .

Тогда

T_i =                                                              (4.1)

В этих обозначениях работа a_i, опирающаяся на работы a_j, a_e, a_k, начнется в момент времени , определяемый из соотношения

,                                 (4.2)

где T_j, T_i, T_k– моменты окончания работ a_j, a_i, a_k.

Применяя формулы (4.1) и (4.2) последовательно для всех работ комплекса табл. 4.1, получим

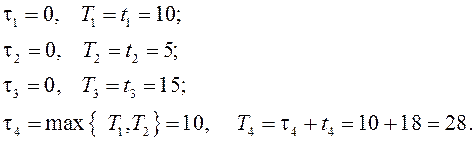      (4.3a)

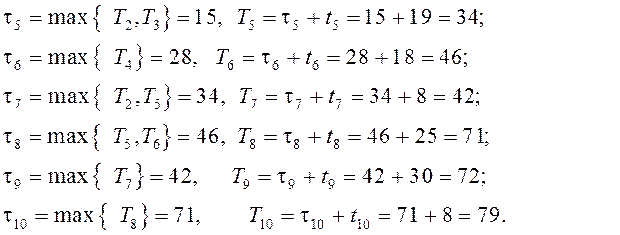(4.3б)

Очевидно, время окончания всего комплекса работ будет

T = max.                                (4.4)

Выражения (4.3), (4.4) представляют формальный алгоритм составления сетевого графика и позволяют провести соответствующий анализ выполнения комплекса работ.

Найдем критические работы (критический путь). Сначала определим работу a_i, для которой T_i = T максимально. Очевидно, эта работа будет критической. Далее, в (4.3) находим . Величина  представлена в виде максимума моментов T_j, T_i,… . Нужно найти тот из них, на котором достигается максимум. Индекс этого момента и даст искомую следующую критическую работу. Данный процесс можно продолжить далее.

Рассмотрим формулы (4.3) и определим критические работы. Очевидно, . Значит работа а₁₀ –  критическая, для которой.