ММ экономических систем, методология исследований. Многокритериальные задачи, преодоление неопределенности целей, страница 6

Простейший (или стационарный пуассоновскийпоток) обладает следующими свойствами.

1. Стационарность– вероятность попадания того или иного числа событий на участок времени τ не зависит от того, где расположен этот участок, а зависит только от его длины. Данное свойство говорит о постоянной плотности потока (среднем числе заявок в единицу времени).

2. Поток является потоком без последействия,если для двух неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий другого участка. Данное свойство говорит о том, что заявки поступают независимо друг от друга.

3. Поток является ординарным, если вероятность попадания двух и более событий на бесконечно малый интервал Δt бесконечно мала. Данное свойство говорит о том, что заявки приходят поодиночке, а не парами, тройками и т. д.

Для других видов потоков пока еще не развиты аналитические методы анализа СМО. Однако доказано, что простейший поток ставит работу СМО в наиболее тяжелые условия и система, рассчитанная для простейшего потока, дает более надежное обслуживание других потоков.

Рассмотрим характеристики простейшего потока. Вероятность того, что за время τ произойдет ровно m событий, равна (распределение по закону Пуассона)

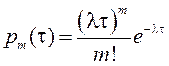, где λ – интенсивность или плотность потока (среднее число событий за единицу времени).

Вероятность того, что за время τ не произойдет ни одного события m = 0, будет

.

Найдем распределение интервала времени T между произвольными соседними событиями. Вероятность того, что на участке времени длины t не появится ни одного события, будет

, а вероятность противоположного события

.

Итак, функция распределения случайной величины Т – промежутка времени между двумя событиями в простейшем потоке будет иметь вид

,                                 (5.1)

а плотность распределения

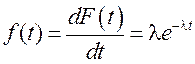.                                   (5.2)

Это есть показательный закон распределения с параметром λ. Математическое ожидание M[T], дисперсия D[T] и среднеквадратическое отклонение σ имеют вид

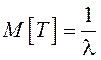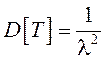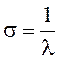, ,.                              (5.3)

Найдем вероятность попадания хотя бы одного события на малый участок длины Δt. В соответствии с (5.1) это будет

.

Или учитывая линейные члены разложения функции в ряд Тейлора при Δt = 0:

,

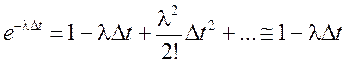получим приближенное выражение

.                                      (5.4)

Основным свойством показательного закона (и только его) является то, что если промежуток времени, распределенный по показательному закону, уже длился некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка. Это фактически и есть отсутствие последействия. Основной характеристикой канала СМО является время обслуживания одной заявки Т_об, которое также является случайной величиной. Будем полагать, что закон распределения времени обслуживания является показательным: f(t) = μe^-μt,где μ – интенсивность потока обслуженных заявок (среднее число обслуженных заявок в единицу времени). Величина μ равна обратному среднему времени обслуживания одной заявки _,  – среднее время обслуживания заявки каналом.

Рассмотрим СМО, в которой протекают только марковские процессы, а переходы системы из состояния в состояние осуществляются под воздействием простейших потоков. Для такой системы можно найти математическую модель в виде линейных дифференциальных уравнений. Получение уравнений рассмотрим на примере СМО, граф которой изображен на рисунке.

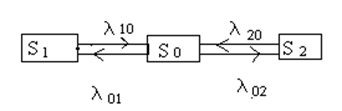
Рисунок

Переход из состояния i в состояние j в системе осуществляется под воздействием простейших потоков событий с интенсивностями λ_ij, (i, j = 0, 1, 2). Граф состояний с проставленными около стрелок интенсивностями называется размеченным.

Вероятностью i-того состоянияназывается вероятность p_i(t) того, что в момент tсистема будет находиться в состоянии S_i. Очевидно, что в любой момент времени tдолжно выполняться равенство

.

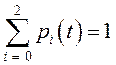Для определения вероятностей состояний p_i(t) данной системы применимы уравнения Колмогорова:

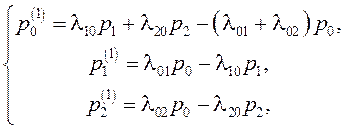                     (5.5)

где для упрощения записано p_i(t) = p_i. При решении уравнений следует учесть условие p₀ + p₁ + p₂ = 1.