Правило составления уравнений Колмогорова: в левой части каждого уравнения стоит производная вероятности i-того события, в правой – сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивность соответствующих потоков событий минус суммарная интенсивность всех потоков, выводящих систему из данного состояния на вероятность данного (i-того) состояния.
Решение системы дифференциальных уравнений
производим, задав какие-то начальные значения (обычно при t = 0)
вероятностей pi(0). Решение уравнений даст зависимость
вероятностей pi(t) как функций времени. При 
имеем предельный
стационарный режим, а значение этих вероятностей pi будем называть предельными или финальными.
Доказано, что если число состояний конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют. Предельная вероятность показывает среднее относительное время пребывания системы в этом состоянии. Например, если p0 = 0,5, то в состоянии S0 в среднем система будет находиться половину времени.
Так как pi = const, то полагая в уравнениях (5.5) 
, получим систему алгебраических уравнений
для стационарного режима:
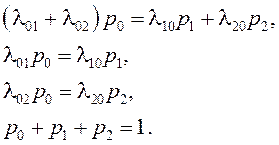(5.6)
При выводе уравнений Колмогорова предполагается, что все потоки с интенсивностями λij, переводящие систему из одного состояния в другое, являются простейшими.
Лекция № 6
Системы массового обслуживания с отказами
Цель работы – изучить способы оценки эффективности работы СМО с отказами.
Теоретические сведения
В СМО с отказами заявка, пришедшая в систему и заставшая все каналы занятыми, покидает ее и в дальнейшем обслуживании не участвует. Первоначально рассмотрим одноканальную СМО. Полагаем, что поток заявок, приходящий в систему, простейший с интенсивностью λ, а время обслуживания канала показательное с параметром μ.
В СМО с одним каналом имеется два возможных состояния: S0 – канал свободен и S1 – канал занят. Размеченный граф представлен на рис. 6.1.
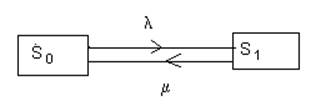
Рис. 6.1
Из S0 в S1 система переходит под воздействием простейшего потока заявок с интенсивностью λ. Из S1 в S0 – за счет потока обслуживаний с интенсивностью μ.
В соответствии с приведенным выше павилом уравнения Колмогорова имеют вид
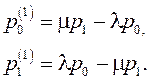
С учетом p0 + p1=1,p1 =1 – p0, первое уравнение будет линейным дифференциальным уравнением
общее решение которого
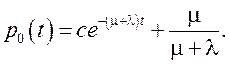
Для вероятности p1 = 1– p0получим
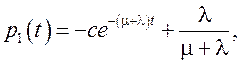
где с – произвольная постоянная.
При t®¥ имеем установившийся режим:
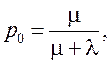
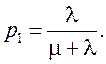(6.1)
Вероятность отказа
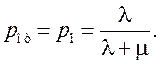(6.2)
Относительная пропускная способность
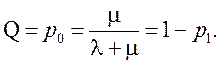(6.3)
Абсолютная пропускная способность
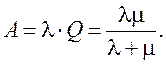(6.4)
Рассмотрим многоканальную систему с отказами, граф которой приведен на рис. 6.2.
Рис. 6.2
Интенсивность перевода из Si в Si+1 постоянна и определяется интенсивностью λ входного потока СМО, а интенсивность обратных переходов из Si+1 в Si неодинакова. Действительно, переход из S2 (два канала заняты) в S1 может осуществиться, если закончит обслуживание либо первый, либо второй канал. Отсюда поток, переводящий СМО из S2 в S1, будет иметь интенсивность 2μ.
Конечные формулы для предельных вероятностей в такой системе (формулы Эрланга)
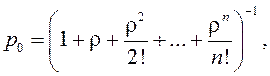p1
= ρp0, 
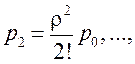
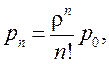(6.5)
где величина ρ = λ ∕μ называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала.
Вероятность отказа СМО
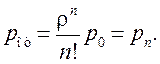(6.6)
Относительная пропускная способность
.
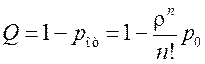(6.7)
Абсолютная пропускная способность
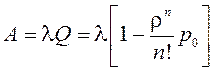. (6.8)
Среднее число занятых каналов можно определить как математическое ожидание дискретной случайной величины, принимающей значения 0, 1, 2,…, n с вероятностями p0, p1, …, pn, т. е.
Подставляя pi из (6.5), получим
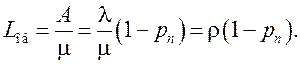(6.9)
Лекция №7
Системы массового обслуживания с ожиданием
Цель работы – изучить способы оценки эффективности работы СМО с ожиданием.
Теоретические сведения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.