Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 9

Непрерывные значения сигнала x(t) преобразуются в диапазоне от х_MINдо х_MAX в моменты времени t в дискретное множество значений x_k - уровней квантования. Здесь квантование по уровню может быть также равномерным и неравномерным. В первом случае весь диапазон сигнала x(t) разбивают на n одинаковых уровней - шагов квантования γ_k, под которым понимают γ_k= x_k - x_k-1, где x_k и x_k-1 — соседние уровни квантования. При равномерном шаге квантования γ_k = (х_MIN– х_MAX)/n. При выбранном шаге квантования возможны следующие способы отнесения значений сигнала x(t) к соответствующему уровню квантования:

сигнал x(t_i) отождествляется с ближайшим уровнем квантования:

сигнал x(t_i) отождествляется с ближайшим меньшим (или большим) уровнем квантования.

На рисунке 1.4-5.4., а показаны два варианта сигналов x₁(t) и x₂(t). Для сигнала x₁(t) при первом способе значение x₁t_i) сигнала принимают равным уровню x_k, по второму способу - равным x_k_₁. По обоим способам значение x₂(t) сигнала принимают равным уровню x_k-1. (Рис. 1.4-5.3. б).

1.4-5.9. Многоуровневое регулирование.

Виды регулирования, о которых мы будем говорить далее, применяются не только в системах обеспечения функционирования источников плазмы. Они характерны для процессов регулирования вообще.

Характерной их особенностью является то, что поведение регулирующего элемента во времени может быть увязано с каким-то известным видом модуляции сигнала. В данном случае управляющего.

Управляющее воздействие не обязательно должно быть монотонным во времени. Достаточно часто оно носит импульсный характер. В простейшем случае оно может быть двухуровневым (клапан в СХПРТ). Естественно, что в таком случае на регулируемую величину кроме модулирующего воздействия будет сказываться и информативность самого процесса, а, кроме того, и инерционность регулирующего устройства. В этом случае результирующее воздействие на характер процесса будет в течении какого-то времени отличатся от вида сигнала, подведенному к регулирующему устройству, т.е. мы будем иметь дело с переходным процессом. Естественно, что регулятор
может иметь и не одно устойчивое положение, а несколько и даже много. В этом случае говорят, что имеет место дискретное регулирование.

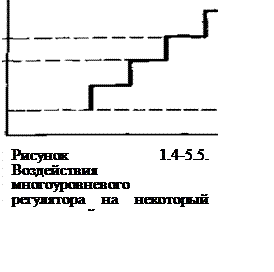
Характер воздействия многоуровневого регулятора на некоторый постоянный параметр можно представить в виде (см. рисунок 1.4-5.5.). Необходимо заметить, что такая же характеристика может быть получена и суммированием импульсных воздействий. Т.е. суммой импульсных амплитудно-модулированных сигналов, у которых (τ_и=Т_и) длительность импульса совпадает с периодом их повторения. В этом случае мы имеем дело с импульсным дискретным регулированием. Понятно, что, управляя параметрами этих воздействующих импульсов, можно синтезировать практически любое воздействие, а кроме этого импульсные системы управления достаточно просто объединить с ЭВМ, если она используется в качестве управляющей системы.

1.4-5.10. Виды модуляции управляющих сигналов.

Под модуляцией в общем случае можно понимать изменение по времени по какому-то определенному закону, какого-то параметра или характеристики сигнала или процесса. При этом не важно, в принципе, что представляет собой управляемый процесс, будь то электрический ток или поток жидкости, газа или плазмы. Важно, правда, знать как изменяются параметры этого процесса или сигнала в невозмущенном состоянии т.к. методы модуляции имеют ограниченное применение и не любой из них применим к любому процессу.

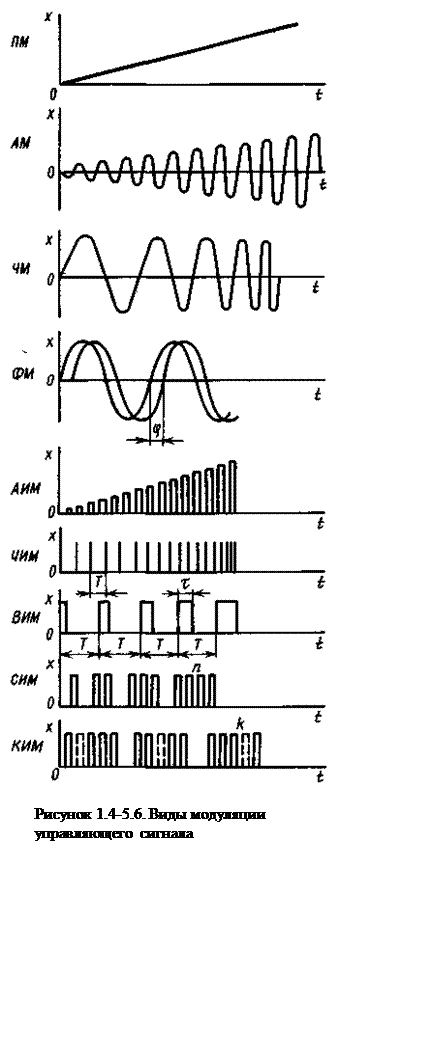
В электротехнике и радиотехнике, которые имеют дело с различным видами электрических сигналов, сложилась вполне определенная терминология, описывающая характер изменения во времени основного сигнала называемого несущей (см. рисунок 1.4-5.6.):

постоянный сигнал Z(t)=X_m;

гармонический сигнал Z(t)=X_m·cos(ω₀t+φ).

Периодическая последовательность импульсов характеризуемая их амплитудой X_m, длительностью τ_m, периодом повторения Т_m.