Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 5

Проблема достижения цели управления относится к вопросам, исследуемым в теории устойчивости. Понятие устойчивости обычно иллюстрируют механической аналогией шарика, находящегося в лунке (устойчивость) или на вершине холма (неустойчивость). В случае если шарик расположен на горизонтальной плоскости, говорят о безразличном состоянии равновесия, или нейтральной устойчивости объекта. Аналогия эта несколько поверхностна. Один из крупнейших математиков прошлого столетия Р. Беллман характеризует термин «устойчивость», как «слово с большой перегрузкой и неустоявшимся определением». Более детальным рассмотрением вопросов устойчивости в ТАУ займемся несколько позже, а здесь рассмотрим, как связаны вопросы устойчивости со второй главной задачей ТАУ - задачей определения закона обратной связи или, как ее еще называют, задачей проектирования оператора обратной связи.

1.4-5.5. Понятие закона обратной связи.

Программная траектория - это траектория, вдоль которой самолет, ведомый автопилотом, никогда не летает. Различного рода возмущения отклонят его от расчетной траектории, поэтому необходима дополнительная система управления, задача которой - устранять воздействия случайных возмущений. Рассмотрим математическую постановку этой задачи в естественном предположении малости возмущений. Поскольку мы знаем  и решение задачи:

                                     (1.4-5.9.)

в отсутствие возмущений, т. е. при , то исходя из предположения о малости возмущений, можно предположить для случая  -

                                    (1.4-5.10.)

Считая  и  величинами того же порядка малости, что и возмущения, подставим (1.4-5.10) в исходную систему (1.4-5.9) линеаризуем ее, т. е. отбросим члены более высокого порядка малости, чем и . В результате несложных выкладок получим

                                      (1.4-5.11.)

где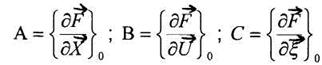 - матрицы, элементами которых являются производные, вычисленные вдоль программной траектории, т.е. при

              (1.4-5.12.)

Понятно, что = 0, а целью корректирующего управления должна быть минимизация модуля или квадрата , что физически соответствует максимизации точности достижения цели . Как и при нахождении программной траектории, необходимо учитывать ограничение по ресурсу управления, причем

                   (1.4-5.13.)

Таким образом, в общем случае задача определения закона обратной связи качественно отлична от задачи программирования. Задаче конструирования обратной связи посвящено огромное число исследований, но до сих пор не созданы общие методы ее решения.

Еще более общую формулировку можно придать данной задаче, задавшись вопросом о нахождении полного множества законов обратной связи, удовлетворяющих системе (1.4-5.11.) и какому-либо критерию точности достижения цели. В такой постановке данная задача носит название задачи синтеза.

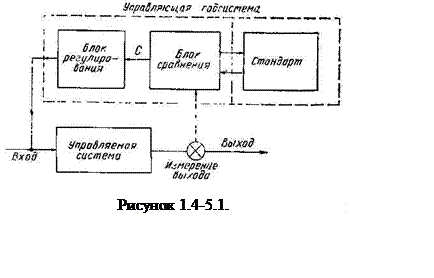
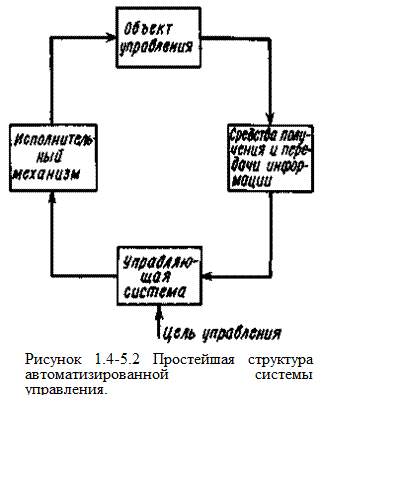
Допустим, что нам удалось решить задачу выбора закона обратной связи, определив , т. е. каким-то образом реализовать схему управления, изображенную на рисунке 1.4-5.1.(в несколько упрощенном виде ее основные слагающие показаны на рисунке 1.4-5.2.). На схеме видно, что сигнал, поступивший на вход объекта управления, преобразуется в нем и результат подается на выход. Через канал обратной связи выход соединен с блоком сравнения, где результат оценивается (например, определяется отклонение С от программной траектории). Допустим, что оно меньше, чем требуется; тогда блок регулирования подает сигнал на увеличение  Наоборот, сигнал от блока регулирования - уменьшение, если результат больше требуемого. В этом процессе и заключается смысл корректирующего управления  или закона обратной связи.