Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 10

Первый из этих сигналов характеризуется только одним параметром - амплитудой, который в данном случае только и можно изменять.

Второй характеризуется тремя параметрами: амплитудой, фазой и частотой (или периодом). То же самое касается и третьего вида сигнала. Именно эти процессы и представляют широкие возможности для управления. Особенно это касается импульсной несущей, где можно менять: амплитуду импульсов, их фазу, частоту повторения, длительность импульсов и пауз, число импульсов в пакете и комбинацию импульсов и пауз, что собственно и представляет собой код. В соответствии с видом основного сигнала различают следующие виды его модуляции:

ПМ – прямая модуляция, изменяющая единственный параметр постоянного сигнала;

АМ – амплитудная модуляция;

ЧМ - частотная модуляция;

ФМ – фазовая модуляция, для гармонического сигнала обозначающая воздействие на его соответствующий параметр;

АИМ – амплитудно-импульсная модуляция;

ЧИМ – частотно-импульсная модуляция;

ВИМ – время-импульсная модуляция;

ШИМ – широтно-импульсная модуляция;

ФИМ – фазоимпульсная модуляция;

СИМ – счетно-импульсная модуляция;

КИМ – кодоимпульсная модуляция.

Они также обеспечиваются воздействием на соответствующий параметр периодической последовательности импульсов, которая является несущей.

На рисунке 1.4-5.6. приведены сигналы, различающиеся видами модуляции для случая равномерного возрастания значения отображаемой величины X(t). Как видно, счетно-импульсная (СИМ) и кодоимпульсная (КИМ) модуляции связаны с квантованием по уровню значений непрерывной величины X. АИМ, ВИМ, ФИМ и ШИМ приводят к дискретности отсчетов во времени.

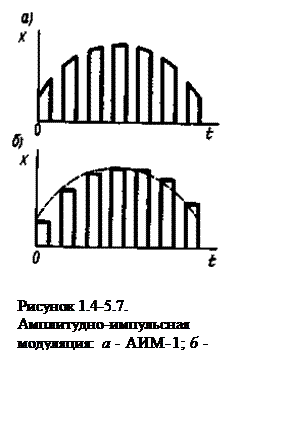
Амплитудно-импульсная модуляция имеет две разновидности:

АИМ-1, при которой амплитуда в пределах одного импульса повторяет форму модулирующего сигнала (рисунок 1.4-5.7.а);

АИМ-2, при которой амплитуда в пределах одного импульса не изменяется и равна значению модулирующего сигнала в момент, соответствующий началу импульса (рисунок 1.4-5.7.б).

В рассмотренных выше примерах, огибающая представляет собой монотонно возрастающую непрерывную функцию. В случае воздействия модулирующего сигнала описываемого более сложной функцией, естественно усложняется и вид результирующей характеристики управляемого процесса. Иногда так, что графически этот процесс достаточно сложно изобразить. Тогда на помощь приходит математика т.к. описать математически можно практически любой процесс управления или модуляции.

Если кривая на рисунке 1.4-5.6. описывает управляющее воздействие, то абсолютно не обязательно, что и характер регулирующего процесса будет абсолютно точно его повторять, т.к. опять таки будет сказываться инерционность и регулирующего устройства, и самое главное, самого регулируемого процесса. Т.е. с учетом инерционности условие τ_и=Т_и становится необязательным. Более того, регулирующее воздействие может состоять из импульсов, фронты которых не соприкасаются. Но результат такого воздействия все равно может быть непрерывной функцией. При инерционном процессе и регулирующем воздействии описываемом, например, АИМ можно получить кривую изменения процесса соответствующую ПМ. Все о чем мы только что говорили, может быть описано математически. Более того, такие описания давно уже имеются. При желании с ним можно познакомиться в соответствующей литературе.

1.4-5.11. Кодирование управляющего сигнала.

Кодирование измерительной информации – это представление сообщений в форме, удобной для ее передачи, приема и хранения. Обратная операция восстановления сообщения по принятому сигналу называется декодированием. При этом под кодом понимают набор правил, по которым составляются отдельные комбинации из элементов.

Элементами кода являются символы и позиции. Число используемых в коде символов образует основание кода m, а совокупность всех позиций – разрядность кода n. Система счисления является частным случаем кода. В зависимости от выбранного основания различают системы счисления двоичную, троичную, восьмеричную и т.д.