Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 7

Условие, задающее область определения функции (1.4-5.18.), следует рассматривать как детерминированное ограничение, т. е. выполняющееся с вероятностью, равной 1.

Несмотря на то, что мы переходим от частной задачи к более общей, физический смысл ранее введенных понятий не изменяется. Но величина платы за управление в виде

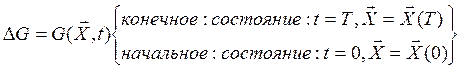
теперь не будет достаточно оправданной и должна быть заменена усредненной величиной, т.е.

                               (1.4-5.21.)

В такой реальной постановке задача становится практически неразрешимой, и на сегодняшний день нет общей математической теории решения таких задач. Поэтому в зависимости от конкретной задачи делают некоторые предположения, позволяющие ее упростить. Одним из таких методов упрощения является схема двухэтапной оптимизации, дающая хорошие результаты в предположении малости возмущений.

Собственно, этот метод проходит в неявном виде через все предыдущее рассмотрение. Поэтому имеет смысл оглянуться назад и посмотреть на изложенное с этой точки зрения.

На первом этапе, при изложении задачи управления, считалось, что ξ = 0, и формулировалась чисто детерминированная задача, в которой J₁ (см. 1.4-5.19.) илиJ₂ (см. 1.4-5.20.) достигали заведомо своего экстремального (минимального или максимального) значения, а плата за управление выражалась чисто детерминированной функцией, т. е. рассматривалась обычная задача оптимального управления:

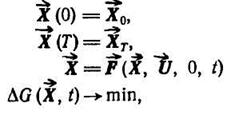                              (1.4-5.22.)

область, в которой требовалось найти программу управления

На втором этапе, считая, что возмущения малы, но не тождественны нулю, искалось корректирующее управление - закон обратной связи, минимизирующий J₁. Разберем этот этап более подробно. Условие (1.4-5.19.) для отклонений Y(t) от программной траектории

                           (1.4-5.23.)

или, что то же,

                                      (1.4-5.24.)

В уравнении (1.4-5.11.) будем считать, что случайный процесс  центрирован, т.е.

                        (1.4-5.25.)

Далее для сокращения записи, используем соотношение (1.4-5.25.), как определение

Ограничиваясь одномерным случаем, имеем для искомых поправок программной траектории и коррекции следующее дифференциальное уравнение:

                            (1.4-5.26.)

с начальным условием у(0) = 0. Из теории дифференциальных уравнений известно, что общее решение данного уравнения равно

                     (1.4-5.27.)

где

Для отыскания корректирующего управления используем формулировку цели управления, данную формулой (1.4-5.23), которая в данном случае будет иметь вид

                                     (1.4-5.28.)

Предполагаем, что корректирующее управление v есть детерминированная функция времени, по аналогии с задачей первого этапа. Подставив (1.4-5.27) в (1.4-5.28), имеем

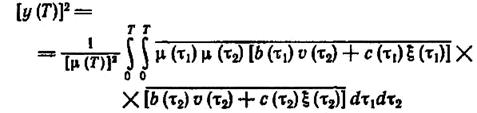                   (1.4-5.29.)

и окончательно получаем из-за центрированности процесса

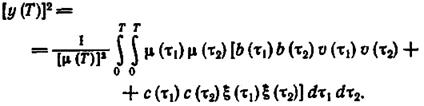        (1.4-5.30.)

Каждое слагаемое в правой части выражения (1.4-5.30.) - положительная величина (сумма квадратов) и, следовательно, в предположении детерминированности корректирующего управления для минимизации условия (1.4-5.28.) необходимо положить v(t) º 0

Результат несколько парадоксальный - для уменьшения ошибки при достижении цели управления надо вовсе не управлять системой. Причину парадокса не надо долго искать. Просто следует корректирующее управление выбирать так, чтобы оно каким-либо способом зависело от возмущения ξ(t). Непосредственно осуществить данное требование технически весьма затруднительно, поскольку для выбора v как функции ξнадо иметь датчики, позволяющие измерять эту величину. Выходом из данной ситуации является косвенный учет зависимости v(ξ), а именно - измерение значений фазовых переменных или их отклонений от программного движения и отыскание корректирующего управления в форме

 или

1.4-5.7. Общие понятия об аналоговом и цифровом регулировании. Реализации дискретного регулирования.