Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 6

Различают положительную и отрицательную обратную связь. Обратная связь считается положительной, если возрастание управляемой величины вызывает ее дальнейшее возрастание, и отрицательной - когда это вызывает ее уменьшение. Соответственно, уменьшение управляемой величины при положительной обратной связи приводит к ее дальнейшему уменьшению, а при отрицательной - увеличивает ее. В ТАУ в большинстве случаев рассматриваются контуры с отрицательной обратной связью.

Реальные системы управления обычно имеют не один, а несколько контуров обратной связи по различным компонентам вектора фазового состояния системы.

Итак, схема управления реализована. Как правило, эта задача носит в большей или меньшей мере характер изобретательства, однако естественно желание иметь некие объективные характеристики предлагаемой системы управления, а также уметь выбирать параметры предлагаемой конструкции. Эти вопросы в ТАУ носят название задачи анализа.

Вернемся к уравнению (1.4-5.11.) и предположим, что нам удалось найти некое допустимое корректирующее управление в виде

                                          (1.4-5.14.)

где Р =(p_ij,) при (i= 1, 2,.... n, j=1, 2,..., r) - матрица конструктивных параметров выбранной нами схемы управления. Основной задачей анализа является определение области (множества) G_Р значений параметров р_ij, при которых решение  асимптотически устойчиво.

Поясним сказанное несколько подробнее: если внешние возмущения отсутствуют, то, очевидно, что . Пусть в некоторый момент времени t = t₀ на объект управления подействовало некоторое случайное возмущение, в результате которого состояние объекта управления изменится:

                                             (1.4-5.15.)

Что будет с объектом управления, после того как помеха исчезнет? Ясно, что если с течением времени отклонение исчезнет, то цель управления будет достигаться. Это математически можно отразить следующим образом:

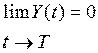                                                     (1.4-5.16.)

в противном случае цель недостижима. Обычно условие (1.4-5.16) записывается в виде:

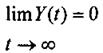                                                    (1.4-5.17.)

Возможность такой замены конечного отрезка времени на бесконечный интервал физически означает предположение о том, что время релаксации (затухания) возмущения во много раз меньше времени управления.Эта замена во многих случаях позволяет провести исследование процесса более простым способом, чем при исследовании его на конечном интервале времени.

Таким образом, зная множество G_P, мы знаем область значений параметров, при которых объект асимптотически устойчив, но поведение объекта, его характеристики будут существенно различны в зависимости от выбора точки множества G_P. Различного рода другие требования, такие как стоимость и простота, технологичность и надежность, будут сужать область допустимых параметров, т. е. G_P перейдет в G_P¹. Очевидно, что если множество G_P¹окажется пусто (т. е. будет «пустым множеством»), то выбранная конструкция должна быть заменена другой. В противном случае в нашем распоряжении остается еще возможность выбора точки на множестве G_P, исходя из какого-нибудь критерия.

1.4-5.6. Общая задача автоматического управления.

Общей задачей ТАУ является задача о стохастической управляемой системе вида

                                         (1.4-5.18.)

Детерминированную цель управления  в этом случае следует заменить некой целью сформулированной в вероятностных терминах, так как фазовый вектор  является случайным. Наиболее распространенными в данных обстоятельствах являются следующие формулировки цели

                  (1.4-5.19.)

т. е. минимизация дисперсии;

                     (1.4-5.20.)

т. е. максимизация вероятности того, что конечное значение фазового вектора находится внутри некоторого достаточно малого интервала  с центром в