Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 4

Первая задача, вернее, один из путей ее решения, основанный на волевом решении главного конструктора, ранее упоминалась. Обсуждение второй задачи — определения закона обратной связи — отложим на некоторое время, так как для этого нам потребуется введение еще некоторых понятий.

Путь решения задачи программирования, когда программная траектория управляемого движения задается, особенно прост и нагляден, если это движение известно заранее (например, поддержание постоянного напряжения на зажимах генератора), или легко рассчитывается (например, изменение курса движущегося судна в зависимости от положения его руля). Остающаяся в нашем распоряжении «свободная» вектор-функция  должна обеспечивать движение объекта по этой траектории, но ее вид может выбираться. Так,  может быть функцией вектора состояния системы  функцией времени   или иметь более общий вид .

Допустим, что имеется некоторое множество управлений, гарантирующих достижение цели; тогда среди них можно выбрать какое-то, наилучшим образом удовлетворяющее (оптимизирующее) некоторому дополнительному требованию. Таким требованием, например, в случае автопилота может быть желание иметь минимальные перегрузки или минимальный расход топлива. Задавая заранее программную траекторию, мы уменьшаем поле (область) оптимизации выбора управления. Поэтому в таких случаях, когда помимо цели управления выдвигается еще некое требование, часто называемое «плата за принятое управление», применяют другой способ решения задачи программирования, а именно ищут допустимое управление, минимизирующее некую плату за управление.

Имеется: математическая модель объекта управления, цель управления и начальное состояние объекта, а также некая функция G(X, t) - математический аналог функции платы за управление, причем

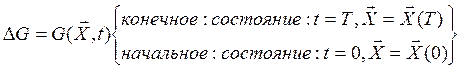                      (1.4-5.7.)

есть плата за принятое управление.

Смысл выражения (1.4-5.7.) заключается в том, что рассматривается на множестве траекторий, переводящих объект из заданного начального состояния (н. с.) в заданное конечное состояние (к. с.) (цель управления), и на этих траекториях вычисляется каждый раз величина, зависящая от н. с. и к. с, и являющаяся платой за управление.

Требуется: найти среди допустимых управлений такое, при котором цель управления достигается, а плата за управление минимальна. Решение  и этой задачи называется программой управления.

1.4-5.4. Описание взаимодействия управляющей системы и объекта автоматического управления.

В реальных условиях на объект управления действуют различного рода возмущения (внешние воздействия). Эти возмущения имеют различную физическую природу и разделяются на два вида: контролируемые и неконтролируемые. Первые в дальнейшем будем обозначать вектором  вторые — . Часто вектор  называют нагрузкой, а вектор — помехой. Вектору  соответствуют возмущения, изменяющиеся по известному закону (например, изменения плотности воздуха с высотой), а вектору — случайные возмущения, такие как порывы ветра или «воздушные» ямы.

Таким образом, в уравнение (1.4-5.1.) эти векторы должны быть введены в качестве аргументов:

                                       (1.4-5.8.)

где -мерный (к< n) вектор возмущений. Нетрудно понять, что если возмущения являются случайной вектор - функцией, то и процесс изменения фазового вектора  будет случайным, что в свою очередь требует уточнения понятий цели управления, платы за управление и др.

Рассмотрим на качественном уровне, к чему приведет действие этих возмущений. Если произойдет ошибка и в результате решения будет найдена не оптимальная программа , то это скажется на увеличении платы за управление (летчик будет испытывать большие перегрузки или произойдет перерасход топлива), но если не принять во внимание возмущения, то скорее всего не будет достигнута цель управления, а это сделает всю нашу работу бессмысленной.