Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 12

Необходимо оговорится, что бывают случаи, когда ЦАП не обязателен. Это реализуется тогда, когда исполнительное устройство имеет два устойчивых состояния. Примером могут быть выключатели или двухпозиционные переключатели в электрических цепях, клапаны в гидравлических и пневмосистемах. Поскольку в таких устройствах два устойчивых состояния, то одному можно присвоить код нуля, а другому единицы. Тогда достаточно, взять сигнал с общей шины ЭВМ и, соответственно усилив его, подать на регулирующий элемент.

Поскольку не все регулирующие устройства обладают двумя устойчивыми состояниями, то это все-таки исключение и в общем смысле преобразование необходимо производить.

Преобразование аналоговой величины в цифровой код является измерительной процедурой и осуществляется путем выполнения ряда операций сравнения измеряемой величины с набором дискретных эталонных величин, имеющих одинаковую природу с преобразуемой.

При этом происходит замена непрерывной величины на ближайшую фиксированную величину из ряда, образованного по определенному алгоритму с помощью меры, и считывание кода, соответствующего этому фиксированному значению.

Одним из критериев, лежащих в основе классификации методов аналого-цифрового преобразования (АЦ - преобразования), является характер АЦ - преобразования во времени. В соответствии с этим критерием различают метод последовательного счета, метод поразрядного уравновешивания, метод одновременного считывания. В основе этой классификации методов АЦ - преобразования лежит характер реализации алгоритма АЦ - преобразования во времени.

Этот критерий, не являясь единственно возможным, приносят наибольшую информацию как при синтезе новой структуры цифрового измерительного прибора (ЦИП), так и при анализе уже имеющейся. Рассмотрим кратко эти методы.

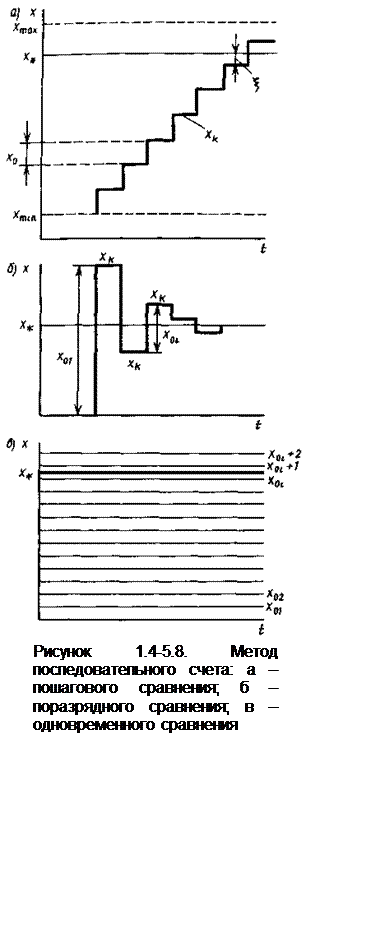
Метод последовательного счета.Сущность метода заключается в последовательном (во времени) сравнении измеряемой величины с известной однородной мерой. Процесс сравнения предполагает дискретное участие в нем меры Х₀ в общем случае как в сторону увеличения текущего значения меры Х_k, так и в сторону его уменьшения. При определении измеряемой величины х:

x.                                 (1.4-5.32.)

Начальные значения х_k в обоих случаях соответственно равны границам диапазона изменения х.

На рисунке 1.4-5.8.а показан первый вариант метода последовательного счета. При некотором числе n квантов х₀ имеет место строгое равенство n·x₀=x_k или с некоторой погрешностью ξ:

,                            (1.4-5.33.)

где х- значение измеряемой величины.

Если выбрать х₀ равным единице измерения х, то число n будет единичным кодом значения измеряемой величины.

Вариантом метода последовательного счета является случай измерения величины, обратной х. При этом в качестве кванта х₀ служит сама преобразуемая величина х и предполагается известной некоторая постоянная величина х_с, которую выбирают так, чтобы 1/х₀ была единицей измерения величины, обратной х. Производя АЦ - преобразование, получим соотношение:

,                         (1.4-5.34.)

тогда очевидно, что n является единичным кодом значения 1/ х. Точность приведенного АЦ - преобразования при прочих равных условиях определяется выбранной величиной х₀, так как погрешность квантования определяется как .

Время АЦ - преобразования при применении метода последовательного счета в общем случае определяется входной аналоговой величиной и находится в обратной зависимости от желаемой точности преобразования, т.е. значения х₀. Таким образом, достоинствами метода являются сравнительная простота и малая статическая погрешность; недостатком – малое быстродействие. Основные области применения метода – цифровые вольтметры постоянного тока и цифровые системы для работы с постоянным и медленно изменяющимися напряжениями. Одна из возможных аппаратных реализаций метода последовательного счета приведена на рисунке 1.4-5.9.