Общие понятия о регулировании в системах обеспечения функционирования источника плазмы, страница 11

Приведем пример. Пусть основание кода m=2, т.е. рассматриваемый код состоит лишь из двух символов 0 и 1, такая система счисления называется двоичной. При основании m=10 (десятичная система счисления) элементарными символами являются цифры от 0 до 9.

Общепризнанным в настоящее время является позиционный принцип образования системы счисления, при этом полное число получается суммированием значения по разрядам:

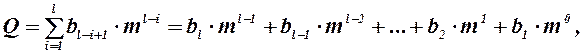(1.4-5.31)

где i-номер данного разряда; l-число разрядов; b_i-множитель, принимающий любые целочисленные значения в пределах от 0 до m-1 и показывающий, сколько единиц i-го разряда содержится в числе.

В измерительной технике наибольшее распространение получила двоичная система счисления, которая технически реализуется значительно проще, чем другие.

Для двоичного кода правила вычитания и умножения следующие:

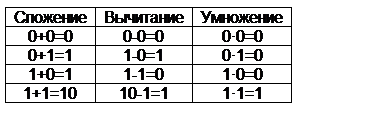Запись в двоичной системе счисления (в двоичном коде) приведена в таблице 1.4-5.1.

Перевод любого десятичного числа в другую систему счисления осуществляется следующим образом. Число в десятичной системе переводится в любую другую систему путем последовательного деления чисел на основании другой системы и выписыванием остатков, которые составляют число в данной системе.

Например, переведем число 27₍₁₀₎ в двоичный эквивалент:

читаем остаток снизу вверх и имеем 27₍₁₀₎=11011₍₂₎.

Число 1101 в двоичной системе счисления переводится в десятичную систему следующим образом:

1101₍₂₎=1·2³+1·2²+0·2¹+1·2⁰=8+4+0+1=13₍₁₀₎.

Учитывая возможные варианты, рассмотреный выше двоичный код называют нормальным.

Двоичный код неудобен при вводе и выводе информации, так как трудно оперировать с непривычными двоичными числами. Кроме того, при больших числах (десятичных) запись двоичного кода становится громоздкой. Поэтому на практике получили распространение такие системы счисления, которые легко сводятся к двоичной, но в то же время сохраняют преимущества десятичных. К ним относятся: восьмеричная, шестнадцатеричная и двоично-десятичная. Последняя получила наибольшее распространение в измерительной технике. Суть ее заключается в том, что каждая цифра десятичного числа (тетрады) представляется четырехразрядным двоичным кодом. При этом наиболее целесообразным кодом тетрады является 8-4-2-1.

В таблице 1.4-5.2. приведен двоично-десятичный код с весами 8-4-2-1.

1.4-5.12. Общие понятия о принципах преобразований код-аналог и аналог-код.

Для управления каким-либо процессом или регулирования отдельной величины очень хорошим средством является вычислительная машина или какая-нибудь микропроцессорная система. Особенно это относится к настоящему времени, когда быстродействие, объем памяти и другие возможности (т.е. параметры) ЭВМ существенно возросли. Однако возникает проблема, как ввести данные с датчика контролируемой величины в ЭВМ и как потом преобразовать сигнал с нее в форму удобную для восприятия исполнительными устройствами.

Понятно, что в качестве промежуточного звена можно использовать человека-оператора. Пусть вручную вводит данные в машину с клавиатуры, и потом, реализует команды ЭВМ, щелкая переключателями или вращая ручки. Это можно сделать, но тогда все преимущество ЭВМ как управляющей системы будет сведено к минимуму т.к. быстродействие человека, как преобразователя информации и исполнительного механизма очень невелико. Кроме того, человеку свойственно ошибаться, а это может привести к последствиям, с которыми ни одна машина не справится.

Наиболее разумно, разумеется, исключить человека из процесса управления или регулирования и преобразования сигналов производить автоматически. Для этого потребуются два устройства, выполняющие обратные функции. Преобразование аналогового сигнала с датчика контролируемой величины в код понятный машине производит аналогово-цифровой преобразователь (АЦП), обратное преобразование – цифро-аналоговый преобразователь (ЦАП), который преобразует код, получаемый из машины в соответствующие уровни напряжения или тока. Этот сигнал, при необходимости, может быть усилен или нормирован специальными усилителями напряжения, тока или мощности и подведен к исполнительному устройству, т.е. к собственно регулирующему устройству.