Математические методы планирования испытаний, страница 9

В большинстве практических случаев вторым членом формулы (3.58) можно пренебречь и для определения дисперсии среднего времени испытаний использовать формулу

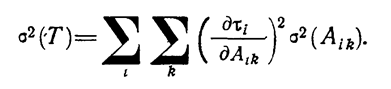                       (1.10-12.59.)

Полученные формулы (1.10-12.54), (1.10-12.59.) могут быть использованы для вычисления среднего времени и дисперсии среднего времени испытаний.

Как видно из этих формул, среднее время испытаний определяется двумя составляющими. Первая составляющая определяет среднее время, необходимое для достижения заданной эффективности: вторая – затраты времени, обусловленные неточностью оценки текущего значения эффективности. Таким образом, сокращение времени испытаний может быть обеспечено за счет увеличения точности оценки параметров, определяющих текущее значение эффективности проектируемой системы.

Выражения (1.10-12.39.), (1.10-12.46.), (1.10-12.54.), определяющие значение текущей эффективности и время, необходимое для достижения заданной эффективности, позволяет получить численные значения критерия (1.10-12.2.), когда под затратами понимается время испытаний.

1.10-12.8. Связь затрат с текущей эффективностью разрабатываемого КА и его систем.

Рассмотренный критерий эффективности испытаний (1.10-12.1.) является техническим критерием, так как не учитывает экономических затрат, необходимых для экспериментальной отработки КА.

Для учета этих затрат необходимо получить зависимости, связывающие затраты с техническим показателем эффективности, а именно, с текущей эффективностью разрабатываемого КА и его систем.

Стоимость разработки образцов ракетно-космической техники зависит от большого числа факторов как технического, так и организационного характера. Такими факторами являются основные технические характеристики проектируемого КА: (масса конструкции, тяга двигателя, сложность аппаратуры), новизна разработки, освоение производства, опыт участвующих в проекте организаций и т. д. Учесть все эти факторы строго не удается, поэтому в качестве математических моделей стоимости обычно используется ряд эмпирических зависимостей, основанных на анализе статистического материала. Кратко остановимся на основных из них.

Как правило, для объектов рассматриваемого класса существуют минимально допустимые значения затрат; при меньших затратах техническая реализация изделия невозможна. Эти затраты назовем базовыми, а соответствующую эффективность – начальной.

Зависимость, связывающую эффективность системы со стоимостью отработки, представляют обычно через начальную эффективность и приращение эффективности как функцию от затрат в виде

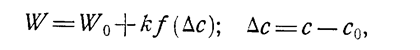                   (1.10-12.60.)

где С₀ - базовые затраты; W₀ - начальная эффективность; k - коэффициент пропорциональности.

Коэффициент k выбирают пропорциональным либо W, либо (1-W), либо W(1-W). Выбор такой формы представления коэффициента k имеет физическую интерпретацию. Покажем это.

Рассмотрим частный случай, а именно, систему постоянного резервирования.

Как известно, вероятность безотказной работы такой системы определяется выражением

                               (1.10-12.61.)

где m – кратность резервирования; W₀ – надежность одного устройства.

Прибавляя и вычитая в правой части (1.10-12.61) W₀, получим

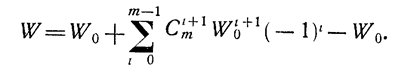
Уравнение 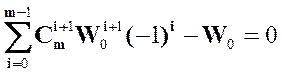 всегда имеет корни W₀ = 1, W₀ = 0.

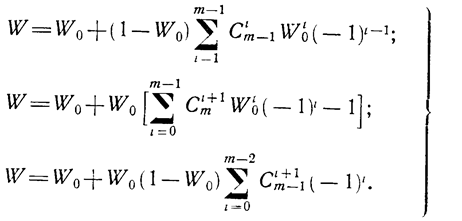            (1.10-12.62.)

Таким образом, считая стоимость пропорциональной кратности резервирования, можно получить следующие выражения для вероятности безотказной работы системы в зависимости от того, какой из коэффициентов пропорциональности используется.

Аналогичные зависимости могут быть получены и для других методов резервирования. В рассмотренном частном случае функция затрат f(Δс) пропорциональна m и выражается через кратность резервирования, которая в общем случае отражает затраты лишь косвенно.