Математические методы планирования испытаний, страница 3

Далее определим P_j(t) как вероятность того, что дефект не был обнаружен еще по прошествии t единиц времени процесса испытаний.

Используя принятые определения, запишем уравнение для вероятности того, что дефект не был обнаружен за время t+dt. Это уравнение будет иметь вид

                          (1.10-12.3.)

где θ_i – интенсивность обнаружения дефектов.

Из уравнения (1.10-12.3.) можно получить дифференциальное уравнение для P_j(t). Для этого проведем цепочку преобразований:

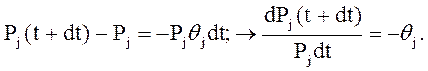
Откуда, собственно, и следует:

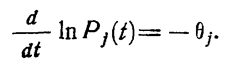                                (1.10-12.4.)

Уравнение (1.10-12.4.) является фундаментальным уравнением для описания процесса обнаружения дефектов.

Решение уравнения (1.10-12.4.) для P_j(t) имеет вид

                                    (1.10-12.5.)

где Р_0j – вероятность необнаружения дефектов к началу j-го испытания.

Распространим теперь данный подход на случай сложной программы испытаний некоторой l-й компоненты, содержащей несколько единичных испытаний, каждое из которых длится время t_j и характеризуется интенсивностью обнаружения дефектов θ_j,. Примем, что число различных единичных испытаний, содержащихся в комбинированном испытании, равно k.

Для такого комбинированного испытания основное уравнение необнаружения дефектов запишется в виде

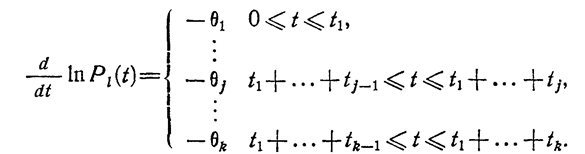(1.10-12.6.)

Полная вероятность необнаружения дефекта в течение всего испытания определяется формулой

    (1.10-12.7.)

Обозначим общее время испытания данной компоненты как

и относительное время, затраченное на каждый j-й тип испытания как

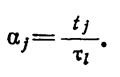
Тогда формулу (1.10-12.7.) можно переписать в следующем виде:

или

                        (1.10-12.8.)

где .

В формуле (1.10-12.8.) величину α_j, можно также интерпретировать как вероятность испытания j - го типа в любой момент в течение всего рассматриваемого комбинированного испытания при условии, что эта вероятность не зависит от времени.

При такой интерпретации величина  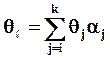есть средняя интенсивность обнаружения дефектов рассматриваемого комбинированного испытания. В отличие от уравнения (1.10-12.8.), которое приводит к кусочно-непрерывному решению для P_l(t), при такой вероятностной интерпретации может быть получено решение при любых t:

                          (1.10-12.9.)

При t = τ_l формулы (1.10-12.8.), и (1.10-12.9.) совпадают.

Следует отметить, что кусочно-непрерывное решение (1.10-12.8.), хотя и требует оценки интенсивности обнаружения дефектов для единичных испытаний каждого типа, является более полным, так как позволяет не только оценить эффективность испытания в целом, но и указать пути повышения этой эффективности.

К сожалению, получение оценок таких индивидуальных значений θ_j затруднительно, так как реальные программы испытаний не всегда предполагают последовательное проведение единичных испытаний различных типов. Эти испытания, могут проводиться одновременно или в какой - либо комбинации. Кроме того, число таких типов испытаний достаточно велико, и дефекты, характерные для каждого отдельного типа испытаний, будут наблюдаться сравнительно редко. Это может привести к тому, что для определения достоверных оценок индивидуальных интенсивностей обнаружения дефектов θ_j, статистического материала по каждому типу испытаний окажется недостаточно. Поэтому для описания модели испытаний компоненты системы на каждом конкретном уровне иерархии испытаний в дальнейшем будет использоваться осредненная модель.

Выражение (1.10-12.9.) определяет закон изменения вероятности необнаружения дефектов при испытаниях некоторой l-й компоненты системы, проведенных на i-м уровне иерархии испытаний.

Перейдем к определению вероятности необнаружения дефекта системы, каждая из k компонент которой подвергалась определенному комбинированному испытанию с интенсивностью θ_j в течение времени τ_l.

Эта вероятность может быть рассчитана на основе известных методов теории надежности. Так, для системы, состоящей из последовательного соединения L компонент, искомая вероятность определится как