Математические методы планирования испытаний, страница 2

Так как сложные технические системы функционируют в условиях, характеризующихся рядом случайных внешних факторов и возмущающих воздействий, а также наличием внутренних «шумов», то в качестве критерия эффективности целесообразно выбрать вероятностный критерий, а именно, вероятность того, что проектируемая система будет отвечать всем предъявляемым к ней требованиям.

При проведении практических расчетов, решении ряда задач планирования и управления процессом экспериментальной отработки изделий наиболее часто используется упрощенная экспоненциальная модель динамики эффективности.

Как показала практика статистической обработки информации, полученной в испытаниях, эта модель достаточно хорошо согласуется с экспериментальными данными.

Эта модель основана на аналогии между понятиями теории надежности и основными характеристиками, определяющими процесс обнаружения дефектов при испытаниях. Данный подход позволяет достаточно просто построить модель динамики эффективности сложных систем по данным испытаний отдельных компонентов. При этом переход к дискретной форме, необходимой для статистического определения основных параметров изменения эффективности, не представляет трудности. Простота зависимостей, связывающих показатели модели динамики эффективности системы с соответствующими показателями составляющими систему компонент, делает непрерывную экспоненциальную модель особенно удобной для решения ряда задач организации процесса экспериментальной отработки.

1.10-12.2. Математическая модель испытаний

Для построения непрерывной математической модели испытаний рассмотрим основные свойства процесса обнаружения дефектов.

Опыт испытаний показал, что дефекты выявляют себя на самых различных этапах программы испытаний. Эти различия во времени обнаружения дефектов могут быть объяснены как специфическими характеристиками самого дефекта, так и характером программы испытаний. Так, например, можно ожидать, что дефекты, чувствительные к термовакуумным условиям, выявляются именно на этапе термовакуумных испытаний и т. д.

Таким образом, процесс обнаружения дефектов может обладать случайными характеристиками, подобными тем, которые рассматриваются в теории надежности. Так, например, время до обнаружения дефекта является аналогом времени до отказа и т. д.

Применяя разработанный в теории надежности математический аппарат, можно получить модель динамики эффективности системы в процессе экспериментальной отработки. Рассмотрим вывод математической модели испытаний в простейшем случае.

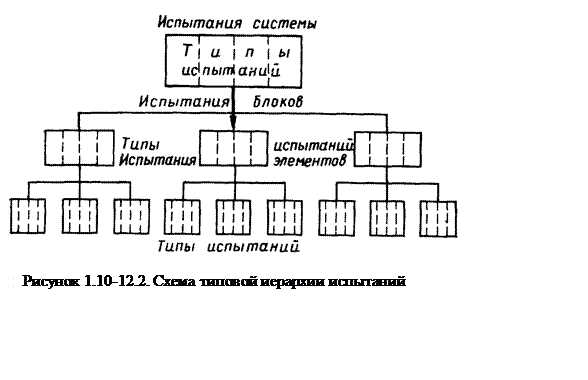
Как уже отмечалось выше, комплексная программа испытаний имеет иерархическую структуру. Программы испытаний на каждом уровне иерархии в свою очередь состоят, как правило, из ряда частных подпрограмм, например из вибрационных, термовакуумных испытаний, испытаний на удар и т. д. (рисунок 1.10-12.2.).

Каждое такое частное испытание определенного типа проводится по единой программе с неизменными условиями испытаний и носит название единичного испытания.

Рассмотрим математическую модель испытания сначала для простейшего случая, когда испытание проводится на некотором j-м уровне, т. е. испытываются отдельные компоненты системы, и испытания этих компонент являются единичными.

При выводе математической модели предположим, что все дефекты одинаковы с точки зрения возможности их обнаружения. В общем случае это не так, потому что вероятность перехода дефекта в отказ и, следовательно, вероятность его обнаружения зависит от условий испытаний.

Предположим также, что дефекты являются независимыми, т. е. вероятность обнаружения дефекта не зависит от числа и вида других дефектов, имеющихся в системе. В ряде случаев, когда один дефект маскирует присутствие другого, это предположение не выполняется.

Для получения математической модели определим Q_j(τ)dτ как вероятность обнаружения дефекта на интервале τ ≤ t ≤ τ+dτ при условии, что на этом интервале проводится единичное испытание j - го типа и что дефект не был обнаружен до момента t = τ. Для единичного испытания Q_j(τ) = const.