Математические методы планирования испытаний, страница 8

Полученные оценки эффективности можно скорректировать введением некоторых масштабных коэффициентов, носящих названия коэффициентов доверия. Эти коэффициенты могут быть определены сравнением оценок эффективности на конкретном уровне испытаний с оценками начальной эффективности на следующем в иерархии уровне. При таком переходе (см. рисунок 1.10-12.9.) наблюдается скачкообразное уменьшение достигнутого уровня эффективности. Это обусловлено переходом на более высокий уровень иерархии системы, когда проявляются новые связи между ее составляющими и реализуются соответственные данному уровню отказы системы.

В качестве иллюстрации рассмотрим возможный способ вычисления коэффициента доверия к результатам наземной отработки. Пусть путем обработки данных испытаний при наземной отработке получена некоторая оценка эффективности  и принято решение о передаче системы для летных испытаний. Значение эффективности, достигнутое при наземной отработке, является начальным значением эффективности для летной отработки. Однако вследствие указанных выше причин оценка начальной эффективности в летных испытаниях , произведенная по результатам этих испытаний, ниже, чем оценка , т. е.

                                              (1.10-12.47.)

Коэффициент доверия к результатам наземной отработки может быть определен как отношение оценок, полученных в наземных и летных испытаниях:

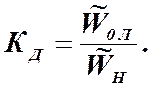                                            (1.10-12.48.)

Коррекцию модели роста эффективности при наземной отработке получаем путем умножения на коэффициент доверия. Для задач планирования летных испытаний, когда эти испытания еще не проведены, для вычисления коэффициентов доверия могут быть использованы данные испытаний систем – аналогов.

1.10-12.7. Определение среднего времени и дисперсии среднего времени испытаний.

Из вышеизложенного следует, что параметры моделей динамики эффективности точно неизвестны, а определяются по результатам испытаний с некоторой погрешностью. Заданная эффективность также может быть определена только в некотором доверительном интервале. Поэтому для получения характеристик общего времени испытаний необходимо определить его среднее значение. Для этого разложим нелинейную функцию (1.10-12.46.) в многомерный ряд Тейлора относительно векторов средних значений параметров .

(Вспомним, что разложение в одномерный ряд Тейлора в окрестности точки имеет вид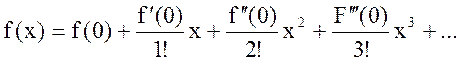, а по степеням малости (х-а) –

)

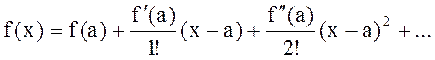При этом элементами вектор-строки являются параметры модели динамики эффективности (1.10-12.38)

Разложение проведем до членов второго порядка включительно. В результате для функции, определенной формулой (1.10-12.46), получим

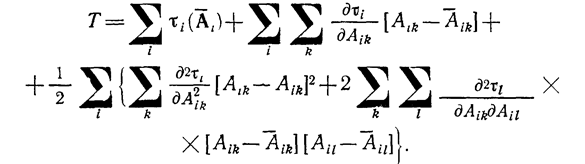          (1.10-12.49.)

В разложении (1.10-12.49.) частные производные

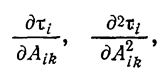
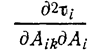
- берутся в точках

Возьмем математическое ожидание обеих частей разложения (1.10-12.49.). В результате получим

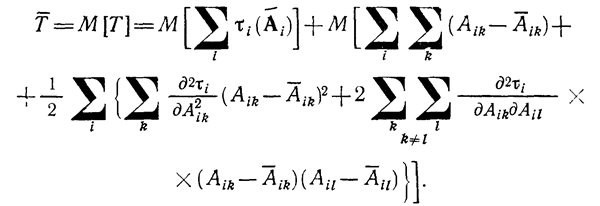          (1.10-12.50.)

В выражении (1.10-12.50.) имеют место очевидные равенства

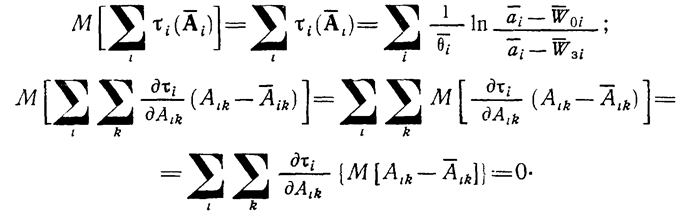(1.10-12.51.)

При условии того, что в качестве оценок  приняты математические ожидания, справедливо равенство

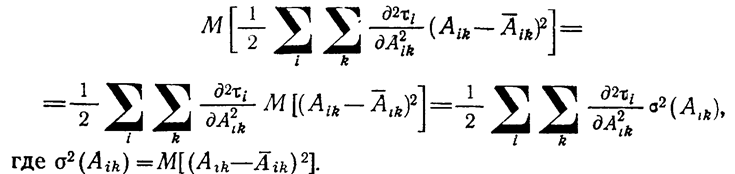(1.10-12.52.)

Далее если параметры  не коррелированны, то соответственно при k ≠ l

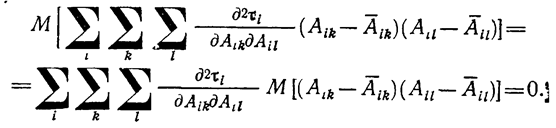(1.10-12.53.)

Учитывая равенство (І.7- 93.51), (1.10-12.52), (1.10-12.53), запишем выражение (1.10-12.50) для среднего времени испытаний в виде

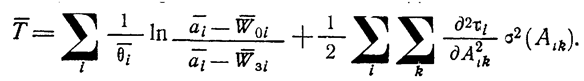(1.10-12.54.)

Для определения точности оценки среднего времени испытаний вычислим его дисперсию

                               (1.10-12.55.)

Возведя обе части формулы (1.10-12.50) в квадрат, применяя к каждому члену, оператор математического ожидания и ограничиваясь членами до третьего порядка включительно, получим

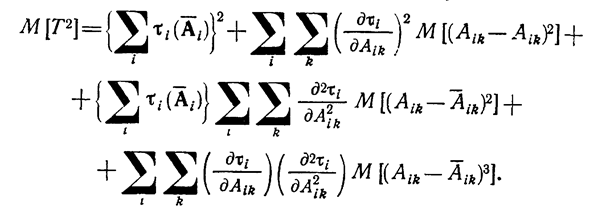(1.10-12.56.)

Учитывая, что второй член формулы (1.10-12.55) равен квадрату формулы (1.10-12.50), запишем выражение для {М[T]}² в виде

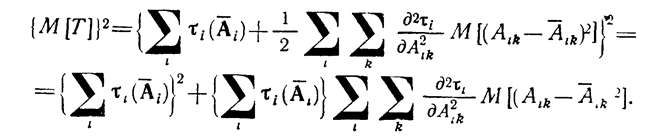(1.10-12.57.)

Используя соотношения (1.10-12.56), (1.10-12.57), запишем выражение (1.10-12.55) для оценки дисперсии σ²(Т):

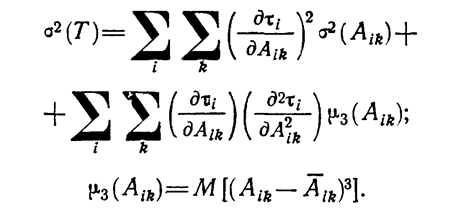                     (1.10-12.58.)