Таким образом, из равенства выражений (1.10-12.26.) и (1.10-12.27.), и (1.10-12.26.) и (1.10-12.28.) следует, что эквивалентная постоянная интенсивность обнаружения дефектов определяется в виде следующих зависимостей:
Для последовательного соединения двух компонент
(1.10-12.29.)
для параллельного соединения двух компонент
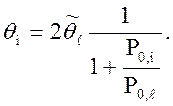(1.10-12.30.)
Аналогичным образом может быть рассчитана эквивалентная постоянная интенсивность обнаружения дефектов и для других структур испытываемых систем.
В случае, когда начальное
значение вероятности необнаружения дефекта 
, что
соответствует отсутствию испытаний, предшествующих исследуемому типу испытаний,
все расчеты значительно упрощаются.
При этом эквивалентная интенсивность для параллельного соединения L компонент может быть вычислена по формуле
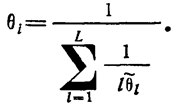(1.10-12.31.)
Эквивалентная интенсивность системы при включении холодного резерва будет
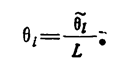(1.10-12.32.)
Полученная в результате применения изложенной методики эквивалентная интенсивность характеризует первую фазу испытаний всякой системы - автономные испытания в составе компонент. Далее система проходит ряд комплексных испытаний, характеризуемых соответствующими значениями интенсивностей обнаружения дефектов. Суммарная интенсивность обнаружения дефектов в такой комплексной программе испытаний рассчитывается, аналогично интенсивности обнаружения дефекта при комбинированном испытании компонент, по соотношению (1.10-12.9.).
Выражением (1.10-12.25.) описывается изменение вероятности необнаружения дефектов в системе при проведении испытаний на i -м уровне иерархии.
1.10-12.3. Описание изменения вероятности необнаружения дефектов в комплексной программе испытаний, проводимых последовательно на различных уровнях иерархии
Применим изложенный подход для описания изменения вероятности необнаружения дефектов в комплексной программе испытаний, проводимых последовательно на различных уровнях иерархии. Полная вероятность необнаружения дефектов для комплексной программы испытаний в целом равна
(1.10-12.33.)
где 0 ≤ t ≤ T ; Р0 = 1 – вероятность необнаружения дефекта к началу программы испытаний; Т -общее время испытаний; θ – средняя для всей комплексной программы испытаний интенсивность обнаружения дефектов. Так как на каждом уровне иерархии испытаний проводится сравнительно большое количество испытаний и наблюдается большое количество дефектов, то имеющаяся в этом случае информация достаточна для достоверной оценки интенсивностей обнаружения дефектов на данном уровне иерархии испытаний.
Поэтому для описания модели всего процесса испытаний в целом воспользуемся не осредненной моделью (1.10-12.33.), а кусочно-непрерывной (1.10-12.8.), позволяющей проводить более детальный анализ эффективности испытаний.
В этом случае
(1.10-12.34.)
где τi
время испытаний на i-м уровне иерархии; n — число уровней
иерархии испытаний.
Из выражения (1.10-12.34.) легко получить текущее значение вероятности обнаружения дефекта на i-м уровне иерархии
(1.10-12.35.)
Сравнивая выражения (1.10-12.34.) и (1.10-12.35.), находим начальное значение вероятности необнаружения дефекта к началу i -го уровня испытаний
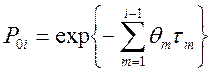(1.10-12.36.)
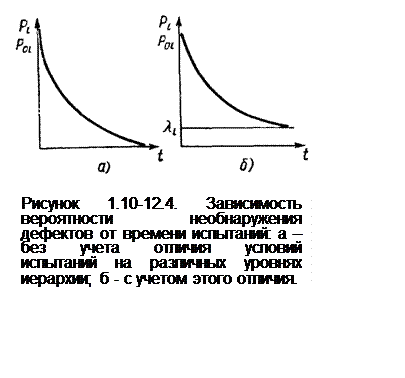
На рисунке 1.10-12.4.а приведена зависимость вероятности необнаружения дефекта на i-м уровне испытаний, рассчитанная по формуле (1.10-12.35.), от времени испытаний.
Как видно из рисунка 1.10-12.4.а, при достаточно большом времени испытания эта вероятность стремится к нулю. Однако в реальных программах испытаний, проведенных на нижних уровнях иерархии, вероятность необнаружения дефектов стремится не к нулю, а к некоторой величине λi, определяющей вероятность наличия в системе дефектов, которые не могут быть обнаружены вследствие несовершенства испытательной программы (рисунок 1.10-12.4.б). С учетом этой величины полная вероятность необнаружения дефектов на i-м. уровне иерархии испытаний может быть представлена в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.