Математические методы планирования испытаний, страница 12

Исходя из сказанного выше, увеличение значений параметров моделей роста эффективности может быть достигнуто за счет модернизации испытательного оборудования, т. е. за счет увеличения базовых затрат. В работе [Волков Л.И., Шишкевич А.М. Надежность летательных аппаратов.- М.: Высшая шк.,1975.- 296 с.] для описания зависимости параметров a_i и θ_i от базовых затрат предлагается использовать модели аллометрического роста

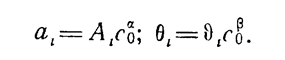                               (1.10-12.84.)

Эти уравнения удовлетворительно описывают связь между параметрами динамики эффективности и базовыми затратами в ограниченном диапазоне изменения последних.

Таким образом, увеличение базовых затрат приводит к снижению необходимого числа испытаний при экспериментальной отработке КА, что экономически выгодно для уникальных объектов космической техники, стоимость единичного испытания которых чрезвычайно высока.

В заключение заметим, что влияние базовых затрат на предельные значения a_i и b_i приводит к более сложной зависимости между текущими затратами и числом испытаний, что необходимо учитывать при планировании экспериментальной отработки сложных технических систем.

Приведенные эмпирические зависимости эффективности от стоимости могут быть проиллюстрированы экспериментальным материалом.

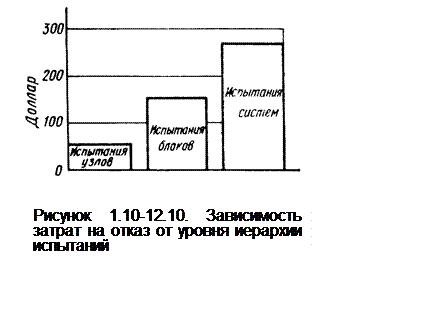
В работах [Koelle D.E. Raumffhrtforschung, 15, Heft 5, s. 182-197 (1971); и 16, Heft 1, s. 1-14 (1972)] отмечается, что коэффициент сложности пропорционален затратам. Таким образом, приведенная выше зависимость надежности от коэффициента сложности (рисунок 1.10-12.7.а) может быть использована также для анализа функции стоимости эффективности и подтверждает ее экспоненциальный характер и повышение предельной стоимости по мере увеличения уровня иерархии. В работе [Fink R.W. Screening for Reliability / Growth-Proceedings Annual Symposium, Los Angeles, 1960, p. 163-172.] приведена величина расходов на отказ в зависимости от уровня иерархии испытаний. Эта зависимость показывает, что расходы увеличиваются приблизительно по экспоненте, что подтверждает уменьшение показателя роста k_i при переходе, на более высокие уровни испытаний (рисунок 1.10-12.10.).

1.10-12.10.2. Средние значения стоимости испытаний.

Параметры модели динамики эффективности в зависимости от стоимости так же, как и в случае зависимости от времени, точно неизвестны и могут быть определены, если зафиксировать значения текущей эффективности и суммы затрат к рассматриваемому моменту и провести статистическую обработку полученных результатов.

Поэтому для характеристики общей стоимости испытаний необходимо определить ее среднее значение. Для этого запишем стоимость i - го уровня испытаний, которая определяется из выражения

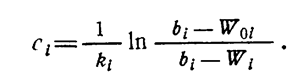                                       (1.10-12.85.)

Общую стоимость комплексной программы испытаний получим путем суммирования стоимостей отдельных уровней иерархии при изменении i = 1, ... N:

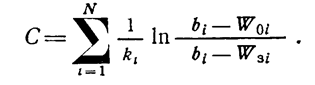                          (1.10-12.86.)

Среднее значение стоимости общей программы испытаний получим, применяя описанный выше метод разложения нелинейной функции (1.10-12.86) в многомерный ряд Тейлора относительно вектора средних значении параметров.

При этом элементами вектор-строки являются параметры модели динамики эффективности

Выражения средней стоимости и ее дисперсии имеют вид

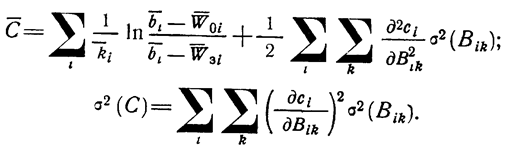(1.10-12.87.-1.10-12.88.)

Выражения (1.10-12.87), (1.10-12.88) показывают, что средняя стоимость так же, как и среднее время, имеет две составляющие, одна из которых определяет стоимость, необходимую на достижение заданной эффективности, а другая зависит от неточности оценки параметров модели динамики эффективности.

Полученные формулы (1.10-12.87), (1.10-12.88) позволяют рассчитывать значения критерия эффективности (1.10-12.2) в случае учета экономических затрат.