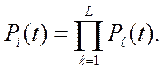 (1.10-12.10.)
(1.10-12.10.)
Для системы, состоящей из параллельного соединения L компонент, эта вероятность будет иметь вид
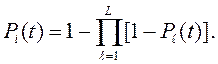 (1.10-12.11.)
(1.10-12.11.)
Для дальнейшего изложения вероятность не обнаружения дефектов в системе удобно представить в обобщенном виде
![]() (1.10-12.12.)
(1.10-12.12.)
Вычислим параметры Р0i и θi(t). Значение начальной вероятности необнаружения дефектов в системе Р0i определяется из выражений (1.10-12.10.), (1.10-12.11.) при t = 0 и для рассмотренных частных случаев имеет следующий вид:
для параллельного соединения
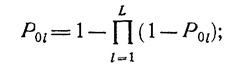 (1.10-12.13)
(1.10-12.13)
для последовательного соединения
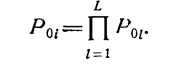 (1.10-12.14.)
(1.10-12.14.)
Значение интенсивности обнаружения дефектов в системе может быть определено из основного уравнения процесса обнаружения дефектов
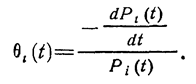 (1.10-12.15.)
(1.10-12.15.)
Для последовательного соединения интенсивность θi определяется наиболее просто и имеет вид
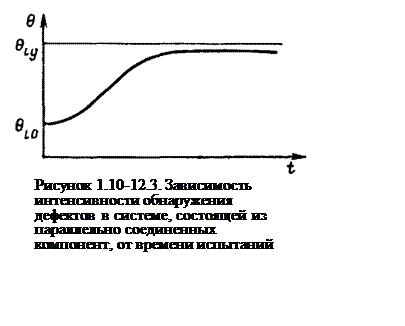
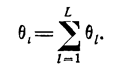 (1.10-12.16.)
(1.10-12.16.)
Определим интенсивность обнаружения дефектов в системе, со стоящей из параллельного соединения L компонент.
Пусть для простоты рассуждений выполняются равенства
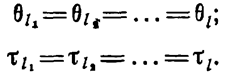
Вероятность обнаружения дефекта в такой системе за время τ определится как
![]() (1.10-12.17.)
(1.10-12.17.)
где![]() .
.
Применяя вероятностную интерпретацию параметров α, получаем при переменном времени t
![]() (1.10-12.18.)
(1.10-12.18.)
где![]() .
.
Дифференцируя выражение (1.10-12.18.), находим плотность вероятности
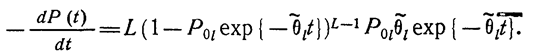 (1.10-12.19.)
(1.10-12.19.)
Интенсивность обнаружения дефектов при испытаниях такой системы вычисляется по формуле (1.10-12.15.) с учетом (1.10-12.19.) и (1.10-12.18.):
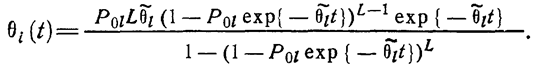 (1.10-12.20.)
(1.10-12.20.)
Из уравнения (1.10-12.20.) следует, что даже при постоянных интенсивностях обнаружения дефектов отдельных компонент интенсивность обнаружения дефектов системы в целом в рассматриваемом примере является возрастающей функцией времени (рисунок 1.10-12.3.). Начальное значение этой интенсивности получается из (1.10-12.20.) и (1.10-12.18.) при t=0
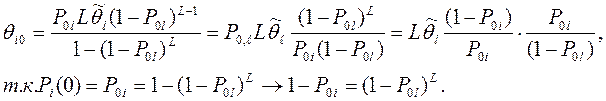
и будет равно
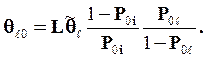
Таким образом, интенсивность обнаружения дефектов в системе меньше интенсивности обнаружения дефектов при испытаниях компонент. Установившееся значение интенсивности, т. е. ее предел на данном уровне иерархии испытаний, равно интенсивности обнаружения дефектов одной компоненты, умноженной на вероятность испытания этой компоненты:
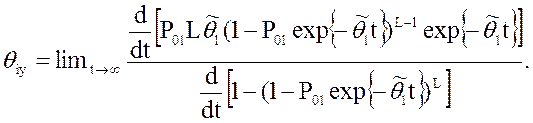 (1.10-12.21.)
(1.10-12.21.)
При анализе вероятности необнаружения дефекта для фиксированного интервала времени, малого по сравнению с общим временем испытаний, можно пользоваться эквивалентной интенсивностью обнаружения дефектов. Приближенное значение эквивалентной интенсивности определится из уравнения
![]() , (1.10-12.22.)
, (1.10-12.22.)
путем разложения соответствующих функций в ряд Маклорена и учета только линейных членов. Так, для случая параллельного соединения двух компонент эта интенсивность будет иметь вид
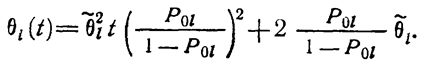 (1.10-12.23.)
(1.10-12.23.)
Для задач анализа комплексной программы испытаний удобно использовать эквивалентную постоянную интенсивность обнаружения дефектов в системе. Определим ее из условия равенства среднего времени до обнаружения дефекта исследуемой системы и ее аппроксимирующей модели.
Среднее время до обнаружения дефекта определяется как
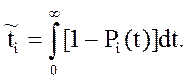 (1.10-12.24.)
(1.10-12.24.)
Если в качестве аппроксимации вероятности необнаружения дефекта в системе принять выражение
![]() (1.10-12.25.)
(1.10-12.25.)
то среднее время до обнаружения дефекта такой системы будет
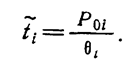 (1.10-12.26.)
(1.10-12.26.)
Для последовательного соединения двух компонент с равными интенсивностями имеем
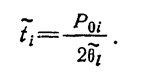 (1.10-12.27.)
(1.10-12.27.)
Среднее время при параллельном соединении двух компонент с равными интенсивностями и начальными условиями будет
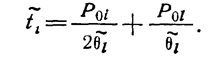 (1.10-12.28.)
(1.10-12.28.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.