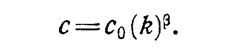Математические методы планирования испытаний, страница 11

                                         (1.10-12.76.)

Выражая k через W и W₀, через цепочку преобразований

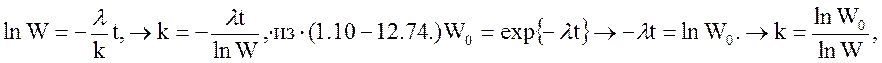получим следующую функцию стоимости:

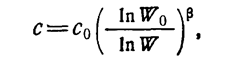                                       (1.10-12.77.)

откуда вероятность безотказной работы в зависимости от стоимости определяется приближенным соотношением

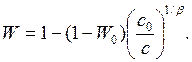                           (1.10-12.78.)

Закон аллометрического (суммарного) роста (1.10-12.76.) является удовлетворительной аппроксимацией только в ограниченном диапазоне значений.

Так, если принять , то уравнение (1.10-12.78.) можно заменить приближенной экспоненциальной зависимостью

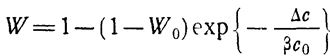                        (1.10-12.79.)

при этом ошибка не превышает 3%.

Заметим, что показатели роста эффективности в зависимости от стоимости в моделях (1.10-12.73.) и (1.10-12.79) обратно пропорциональны базовым затратам С₀, т. е. при достаточно высоких базовых затратах влияние текущих затрат на эффективность системы уменьшается. Действительно, практика проектирования показывает, что базовые затраты являются косвенным показателем сложности системы, а чем сложнее система, тем большие текущие затраты необходимы на ее дальнейшее совершенствование.

Зависимость эффективности от стоимости (1.10-12.73.) удобно использовать для описания затрат на проведение всей комплексной программы испытаний. Для того чтобы описать затраты на отдельных этапах экспериментальной отработки, в уравнении (1.10-12.73) необходимо учесть, что предельные значения эффективности на отдельных этапах b_i < 1 и каждый этап характеризуется своим показателем роста эффективности. Учитывая это, приходим к следующей эмпирической зависимости текущей эффективности от стоимости затрат на отдельном i -м этапе испытаний:

,             (1.10-12.80.)

где b_i – предельное, по стоимости, значение эффективности на i – том уровне иерархии испытаний, k_i - показатель роста эффективности.

1.10-12.10. Особенности динамики эффективности в зависимости от стоимости.

Остановимся на особенностях динамики эффективности в зависимости от стоимости, характерных для отдельных этапов испытаний.

Предельные по стоимости значения b_i определяются возможностями современной техники имитировать на данном i-м этапе реальные эксплуатационные условия. Чем ниже уровень, на котором проводятся испытания, тем меньше соответствующие значения b_i, так как испытания при более высоких уровнях сборки характеризуются более полной имитацией эксплуатационных условий. Показатель роста эффективности k_i уменьшается при переходе на более высокие уровни. Это объясняется большими затратами, необходимыми для устранения дефектов на этих уровнях.

Таким образом, указанные особенности можно записать в виде неравенств

                                  (1.10-12.81.)

Общая стоимость разработки определяется суммой базовых и текущих затрат

                                              (1.10-12.82.)

Базовые затраты С₀ также оказывают влияние, на эффективность разрабатываемого изделия, однако математическая модель этого влияния более сложная.

1.10-12.10.1. Зависимость эффективности от базовых затрат.

Остановимся более подробно на зависимости эффективности от базовых затрат.

Наиболее универсальная модель роста эффективности на отдельном i-м этапе в зависимости от времени или, в дискретном варианте, от числа испытаний определяется соотношением

Полученные соотношения эффективности в зависимости от стоимости (1.10-12.73), (1.10-12.79) и эффективности от числа испытаний (1.10-12.79.) позволяют установить пропорциональную зависимость между стоимостью повышения эффективности и числом испытаний

                                          (1.10-12.83.)

Причем параметры динамической модели W(n_i) определяются техническими возможностями испытательного оборудования, применяемого на конкретном предприятии. В общем случае величины параметров a_i и θ_i не больше, чем величина аналогичных параметров b_i и k_i модели стоимости эффективности. Равенство достигается, когда предприятие применяет наиболее совершенное для данного уровня развития техники испытательное оборудование.