Математические методы планирования испытаний, страница 10

При любом способе избыточности неизбежны общие элементы. Например, при постоянном резервировании такими общими элементами являются шасси, корпуса и т д. Поэтому желательно представить функцию затрат выражением достаточно общего вида с учетом указанного обстоятельства и, в то же время, позволяющего аппроксимировать затраты для отдельных частных случаев.

Как показано в работе [Джиндорф Т., Деврие Т. Роль испытаний при разработке космических аппаратов «Маринер».- Вопросы ракетной техники, 1971, № 10, с. 3-12.], из рассмотренных выше форм представления стоимости наиболее удобной является форма записи с коэффициентом k= (1-W₀):

                                         (1.10-12.63.)

Аппроксимирующая функция f(Δс), исходя из общих свойств надежности W, должна удовлетворять следующим условиям:

W=W₀ при Δc=0, т.е f(Δc)=0;

W=1 при Δc→∞, т.е lim f(Δc)|_Δc→∞ =1                     (1.10-12.64)

Этим условиям, например, удовлетворяет функция вида

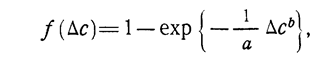                                    (1.10-12.65.)

где коэффициенты а и b определяют конкретное значение функции затрат.

Таким образом, для описания зависимости изменения эффективности от затрат можно пользоваться уравнением вида

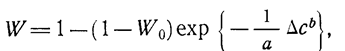                               (1.10-12.66.)

откуда Δс, через цепочку преобразований

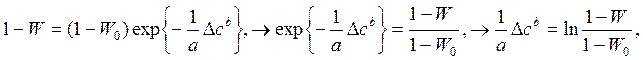
определяется как

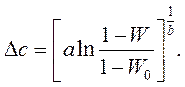                                                (1.10-12.67.)

Условиям (1.10-12.64.) удовлетворяет ряд других функций, например, функция

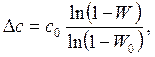                                           (1.10-12.68.)

которая используется в работе [Шастова Г.А., Коекин А.И. Выбор и оптимизация структуры информационных систем.- М.: Энергия, 1972.- 239 с.] для описания зависимости между стоимостью и вероятностью безотказной работы при постоянном резервировании.

Как следует из формул (1.10-12.67) при b = 1 и (1.10-12.68.), между приращением стоимости и приращением эффективности существует приблизительно пропорциональная зависимость.

Действительно, разлагая правую часть выражений (1.10-12.67.) и (1.10-12.68.) в ряд Тейлора относительно точки W₀, можно получить соответственно

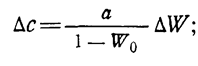                                    (1.10-12.69.)

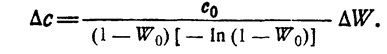              (1.10-12.70.)

Постоянное (горячее, нагруженное) резервирование занимает особое место среди прочих методов резервирования. По материалам [Шастова Г.А., Коекин А.И. Выбор и оптимизация структуры информационных систем.- М.: Энергия, 1972.- 239 с.] его можно считать менее экономичным методом повышения эффективности, чем повышение эффективности путем устранения дефектов проектирования и изготовления, выявленных при испытаниях. Поэтому функцию стоимости при горячем резервировании можно принять в качестве верхней границы модели стоимости испытаний. Исходя из этих соображений, функция затрат на устранение дефектов, может быть получена из выражения (1.10-12.68.) путем понижения основания логарифма в соответствии с правилом

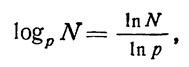                                     (1.10-12.71.)

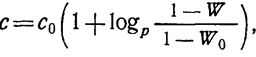                          (1.10-12.72.)

где 0 ≤ p ≤ 1-W₀.

При р = 1-W₀ приходим к выражению (1.10-12.68.).

Из уравнения (1.10-12.72.) можно получить экспоненциальную зависимость эффективности от стоимости:

                     (1.10-12.73.)

где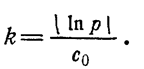

1.10-12.9. Модель стоимости, основанная на анализе влияния доработок на интенсивность отказов системы.

В работе [Шастова Г.А., Коекин А.И. Выбор и оптимизация структуры информационных систем.- М.: Энергия, 1972.- 239 с.] предложена модель стоимости, основанная на анализе влияния доработок на интенсивность отказов системы. Пусть до проведения доработок вероятность безотказной работы системы описывалась зависимостью

                                    (1.10-12.74.)

Проведение доработок привело к уменьшению интенсивности отказов в k раз, т. е.

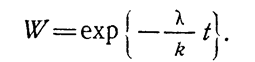                           (1.10-12.75.)

Затраченная стоимость связана с коэффициентом уменьшения отказов моделью аллометрического (суммарного) роста