![]() (1.10-12.37.)
(1.10-12.37.)
1.10-12.4. Модель динамики эффективности в процессе экспериментальной отработки КА.
С помощью зависимости (1.10-12.37.) возможно получение модели динамики эффективности в процессе экспериментальной отработки КА. Обнаружение дефекта и отказ в системе КА, вызванный этим дефектом, являются несовместными событиями, образующими полную группу событий, т. е. сумма их вероятностей равна единице
![]() (1.10-12.38.)
(1.10-12.38.)
где 1 — Pi(t) — вероятность обнаружения дефекта; Ri(t) = 1-Wi(t) – вероятность отказа в системе; Wi(t) – вероятность безотказной работы (эффективность).
В соответствии с принятым нами выше определением эффективности, подставляя в выражение (1.10-12.38.) соотношения (1.10-12.37) и (1.10-12.33), получим
![]() .
.
Учтем, что 1-λi=ai. После подстановки , получим
![]()
для дальнейших преобразований,
рассмотрим это выражение для момента времени ![]() ,
, ![]() , откуда
, откуда ![]()
Произведя подстановку, получим зависимость для определения эффективности системы в виде
![]() (1.10-12.39.)
(1.10-12.39.)
где аi =1- λi
- предельное для данного i-го уровня испытаний значение эффективности;![]() - значение эффективности к началу i-го
уровня испытаний.
- значение эффективности к началу i-го
уровня испытаний.
Этот вывод можно представить следующим образом:
![]()
Для момента времени, ![]() Откуда и следует:
Откуда и следует: ![]()
Из уравнения (1.10-12.39.)
видно, что изменение эффективности при испытаниях на i-м уровне подчиняется
экспоненциальному закону с постоянным темпом. При этом скорость возрастания
эффективности для экспоненциальной модели динамики (1.10-12.39.)
пропорциональна обнаруженной в процессе испытания ненадежности в данный момент
времени 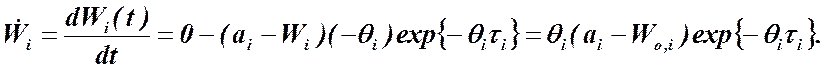
Из ![]() Проведя
подстановку, получим
Проведя
подстановку, получим
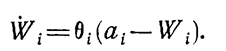 (1.10-12.40.)
(1.10-12.40.)
 Так как в системе имеется ограниченное
число дефектов, то скорость роста эффективности с течением времени вследствие
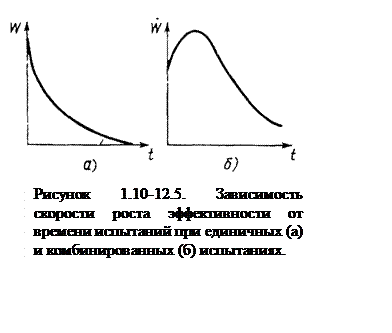
уменьшения числа оставшихся в изделии дефектов монотонно убывает (рисунок 1.10-12.5.а).
Так как в системе имеется ограниченное
число дефектов, то скорость роста эффективности с течением времени вследствие
уменьшения числа оставшихся в изделии дефектов монотонно убывает (рисунок 1.10-12.5.а).
Как отмечалось выше, реальная программа испытаний состоит из некоторой комбинации единичных испытаний, причем эти единичные испытания располагаются обычно в порядке возрастающей интенсивности условий испытаний. В этом случае следует ожидать, что осредненная скорость роста эффективности системы будет сначала возрастать за счет более жестких условий, способствующих выявлению дефектов, а затем убывать из-за уменьшения числа оставшихся в системе дефектов (рисунок 1.10-12.5.б).
Для того чтобы получить модель эффективности системы, удовлетворяющей условию наличия экстремума скорости роста изменения эффективности, наложим условие
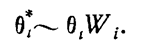 (1.10-12.41.)
(1.10-12.41.)
Из (1.10-12.41.) следует, что интенсивность обнаружения дефектов в процессе испытаний увеличивается вместе с возрастанием эффективности. В результате может быть получена т. н. логистическая модель эффективности системы в виде
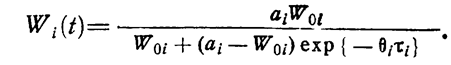 (1.10-12.42.)
(1.10-12.42.)
Для этой модели скорость роста эффективности определяется соотношением
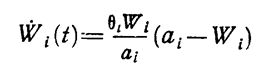 (1.10-12.43.)
(1.10-12.43.)
и имеет максимум в точке
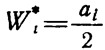
Обе модели динамики эффективности - экспоненциальная и логистическая известны также в общей теории систем, где они применяются для описания процессов развития сложных систем.
1.10-12.5. Особенности моделей динамики эффективности, характерных для отдельных уровней иерархии испытаний
Остановимся на особенностях моделей динамики эффективности, характерных для отдельных уровней иерархии испытаний.
Предельные значения эффективности системы ai, которые могут быть получены в результате проведения испытаний на i-м уровне, определяются степенью адекватности условий испытаний реальным эксплуатационным режимам. На низших уровнях иерархии величина ai меньше, чем на более высоких уровнях иерархии испытаний. Это объясняется тем, что при переходе на высшие уровни испытаний появляются специфические дефекты, присущие только этим уровням. Эти дефекты обусловлены взаимодействием компонент сложной системы и не могут быть выявлены на низших уровнях. Поэтому испытания на низших уровнях дают сравнительно низкую гарантию безотказной работы системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.