



















R2 = R4 = 40 Ом, Е = 100 В, J1 = 0,2×I1, J2 = 0,5×I2. Сделать проверку по второму закону Кирхгофа.
Задачу решим методом контурных токов. В качестве контурных токов взяты: II = J1, III = J2, IIII = I1; направления обхода контуров показаны на рис. 1.61.
Токи ветвей, являющиеся управляющими, запишем через контурные токи: I1 = IIII; I2 = III + IIII. Тогда токи управляемых источников (они же и контурные токи):
II = J1 = 0,2×I1 = 0,2×IIII; III = J2 = 0,5×I2 = 0,5×III + 0,5×IIII.
Из последнего уравнения вытекает, что III = IIII.
Поскольку неизвестным считается только один контурный ток (IIII), для него и составляем контурное уравнение:
(R1 + R2 + R3 + R4)×IIII– (R3 + R4)×II + (R2 + R3)×III = E
или (R1 + R2 + R3 + R4)×IIII– (R3 + R4)×0,2×IIII + (R2 + R3)×IIII = E.
Отсюда третий контурный ток:
IIII=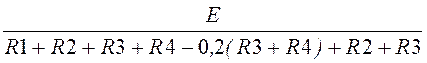 =
=
=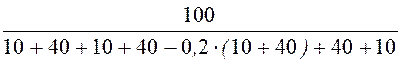 =
0,714 А.
=
0,714 А.
Токи управляемых источников (остальные контурные токи):
J1 = II = 0,2×IIII = 0,2×0,714 = 0,143 А; J2 =III =IIII = 0,714 А.
Токи ветвей, выраженные через контурные токи:
I1 = IIII = 0,714 А; I2 = III + IIII = 0,714 + 0,714 = 1,428 А;
I3 = III + IIII – II = 0,714 + 0,714 – 0,143 = 1,285 А;
I4 = IIII – II = 0,714 – 0,143 = 0,571 А.
Уравнение, составленное по второму закону Кирхгофа для третьего контура имеет вид:
R1×I1 + R2×I2 + R3×I3 + R4×I4 = Е.
Подставим числовые значения:
10×0.714 + 40×1.428 + 10×1.285 + 40×0.571 = 99,95 » 100 В.
2. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Между величинами, характеризующими электрические и магнитные цепи, существует формальная аналогия:
Электрические цепи |
Магнитные цепи |
|
Ток I, А |
Поток Ф, Вб |
|
ЭДС Е, В |
МДС F=I×W, А |
|
Сопротивление r, Ом |
Магнитное сопротивление RM, 1/Гн |
|
Напряжение U, В |
Магнитное напряжение UM=H×l, А |
Эта формальная аналогия распространяется и на уравнения, описывающие состояние цепей:
- первый закон Кирхгофа: SI= 0, S Ф = 0;
- второй закон Кирхгофа: SUr= S Е, SUМ= SF;
- закон Ома:Ur=I×r,UМ= Ф×RM ;
причём в последних выражениях используются статические сопротивления электрических элементов (r) и магнитных элементов (RM).
Свойства нелинейных элементов определяются их характеристиками: электрических – вольтамперными U= f(I), магнитных – вебер-амперными Ф = f(UM).
Системы уравнений, описывающих состояние цепей, составляются с помощью законов Кирхгофа. С точки зрения математики – это нелинейные алгебраические уравнения, для разрешения которых применяются различные приближённые методы, которые в курсе ТОЭ называют методами расчёта нелинейных цепей.
Наиболее часто употребляются:
1) графические методы;
2) графо-аналитические методы;
3) численные методы.
2.1. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Свойства нелинейных элементов определяются их вольтамперными характеристиками и в рассматриваемых задачах анализа электрических цепей считаются заданными: либо снятыми экспериментально с помощью вольтметров и амперметров, либо определяются паспортными данными по каталогам или данным заводов-изготовителей.
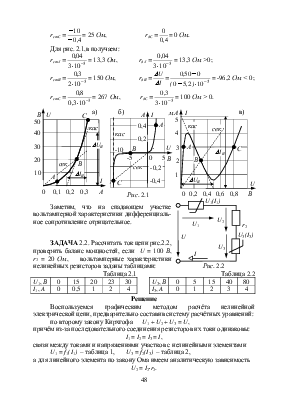
ЗАДАЧА 2.1. На рис. 2.1,а приведена вольтамперная характеристика лампы накаливания с вольфрамовой нитью, на рис. 2.1,б – стабилитрона, на рис. 2.1,в – туннельного диода. Для указанных точек (рабочих точек устройства, точек равновесия) определить статические и дифференциальные сопротивления элементов.
Проведём через указанные точки секущие из начала координат (сек) и касательные (кас). Для рис. 2.1,а получаем:
rстА =![]() =
=![]() = 30 Ом,rдА =
= 30 Ом,rдА =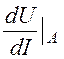 = lim
= lim![]() =
=![]() =
45,5 Ом;
=
45,5 Ом;
rстВ =![]() =
=![]() = 83,3 Ом,rдВ =
= 83,3 Ом,rдВ =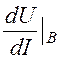 =
=![]() = 250 Ом;
= 250 Ом;
rстС =![]() =
=![]() = 156,3 Ом,rдС =
= 156,3 Ом,rдС =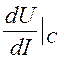 =
=![]() = 385 Ом.
= 385 Ом.
Для рис. 2.1,б получаем:
rстА =![]() =
6,25 Ом,rдА =
=
6,25 Ом,rдА =![]() = 0,25 Ом;
= 0,25 Ом;
rстВ =![]() =
¥ Ом, rдВ =
=
¥ Ом, rдВ =![]() =
¥ Ом;
=
¥ Ом;
rстС =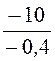 =
25 Ом, rдС =
=
25 Ом, rдС =![]() = 0 Ом.
= 0 Ом.
Для рис. 2.1,в получаем:
rстА =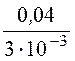 =
13,3 Ом, rдА =
=
13,3 Ом, rдА =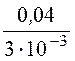 = 13,3 Ом >0;
= 13,3 Ом >0;
rстВ =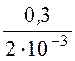 =
150 Ом, rдВ =
=
150 Ом, rдВ =![]() =
=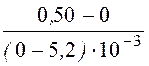 = -96,2 Ом < 0;
= -96,2 Ом < 0;
 |
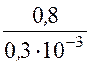 =
267 Ом,rдС =
=
267 Ом,rдС =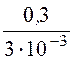 = 100 Ом > 0.
= 100 Ом > 0.
Заметим, что на спадающем участке вольтамперной характеристики дифференциаль-ное сопротивление отрицательное.
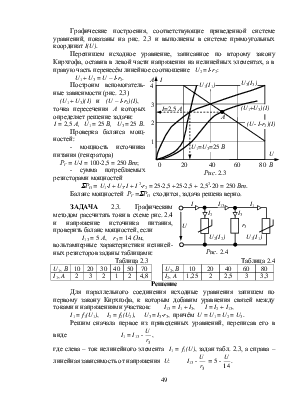
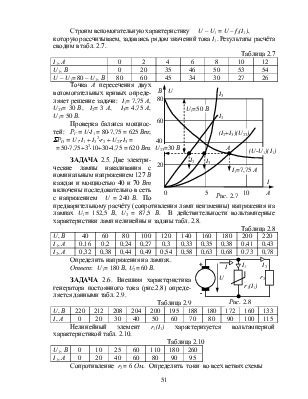
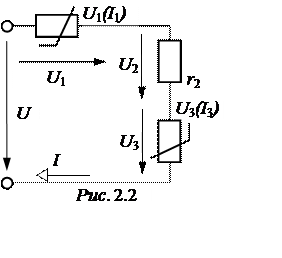
ЗАДАЧА 2.2. Рассчитать ток цепи рис.2.2, проверить баланс мощностей, если U= 100 В, r2 = 20 Ом, вольтамперные характеристики нелинейных резисторов заданы таблицами:
|
U1, В |
0 |
15 |
20 |
23 |
30 |
U3, В |
0 |
5 |
15 |
40 |
80 |
|
|
I1, A |
0 |
0,5 |
1 |
2 |
4 |
I3, A |
0 |
1 |
2 |
3 |
4 |
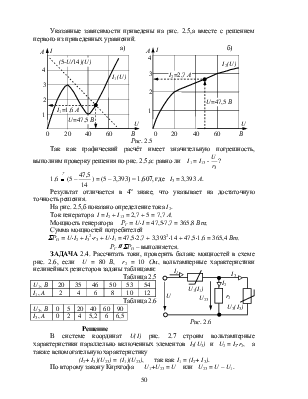
Воспользуемся графическим методом расчёта нелинейной электрической цепи, предварительно составив систему расчётных уравнений:
по второму закону Кирхгофа U1 + U2 + U3 = U, причём из-за последовательного соединения резисторов их токи одинаковы:
I1 = I2 = I3 = I, связи между токами и напряжениями участков с нелинейными элементами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.