Нелинейные электрические и магнитные цепи постоянного тока, страница 8

Силу тяги электромагнита на один воздушный зазор рассчитаем по методу возможных перемещений (см. курс «Прикладная механика»). Энергия магнитного поля в воздушном зазоре

W_В =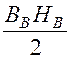V_B =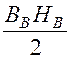×S_В×l_В.

При бесконечно малом перемещении якоря изменяется длина воздушного зазора при неизменных В_В, Н_В. Сила притяжения якоря к сердечнику на один воздушный зазор

F₁ = -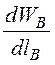= -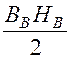×S_В.

Сила тяги электромагнита на два воздушных зазора

F = |2×F₁| = В_В×H_В×S_В =×S_В = 0,8×10⁶×В_В²×S_В.

В рассматриваемом примере

F = 0,8×10⁶×1,1²×20×10^-4 = 1936 Н » 198 кГ.

Отрывную силу электромагнита определим из условия, что при задан-ной намагничивающей силе  IW =1034 А  воздушный зазор отсутствует l_В= 0.

Тогда при S_С= S_Я= Sи однородном материале магнитопровода

H_С= H_Я =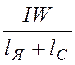==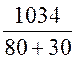 9,4 А/см.

По   кривой   намагничивания   соответствующая  магнитная   индукция В = 1,357 Тл,  отрывная сила электромагнита

F_отр= 0,8×10⁶×1,357²×20×10^-4 = 2946 Н » 300 кГ.

ЗАДАЧА 2.21. Левый магнитопровод (рис. 2.25) имеет воздушный за-зор l_В= 0,11 см, правый – без воздушного зазора. Средние длины магнито-проводов l₁= l₂= 60 см, сечения S₁= S₂= S_В= 6 см². Магнитный поток левого сердечника Ф₁ = 6,6×10^-4 Вб. Материал магнитопроводов – электротехниче-ская сталь 1512, кривая намагни-чивания которой задана  таблицей в задаче 2.18.

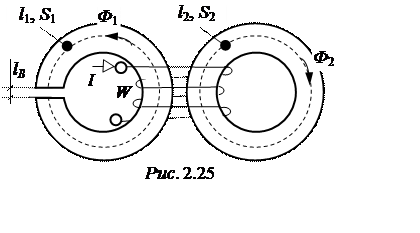Определить МДС обмотки и магнитный поток Ф₂.

Ответы:IW = 1148 А,

Ф₂ = 8,88×10^-4 Вб.

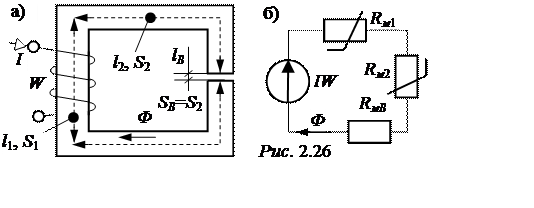
ЗАДАЧА 2.22. Сердечник неразветвлённой магнитной цепи рис. 2.26,а выполнен из электротехниче-ской стали 1512, кривая намагничивания которой приведена в задаче 2.18. Размеры сердечника:  l₁ = 20 см,  S₁ = 6 см²,     l₂ = 40 см,   S₂ = S_В = 4 см²,l_В= = 1,2 мм.  Число витков катушки   W =500,  ток   I = 5 А.

Построить схему замещения магнитной цепи; рассчитать магнитные индукции каждого участка магнитной цепи; определить запас энергии магнитного поля каждого участка и суммарный запас энергии цепи.

Решение

Схема замещения катушки с ферромаг-нитным сердечником, аналогичная электриче-ской цепи, приведена на рис. 2.26,б. Расчёт магнитного потока осуществляется методом последовательным приближений. Для первого шага приближения примем произвольное значение В₂ = В_В = 1,2 Тл, при котором Н₂ = 4,65 А/см на основании кривой намагничивания, а

Н_В = 0,8×10⁴×В_В = 0,8×10⁴×1,2 = 0,96×10⁴ А/см.

Магнитный поток катушки при этом

Ф = В₂×S₂= 1,2×4×10^-4 = 4,8×10^-4 Вб,

Магнитная индукция и напряженность на первом участке сердечника

В₁ ===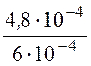 0,8 Тл,      Н₁ = 1,15 А/см.

Намагничивающая   сила,   необходимая   для   создания   потока    Ф = = 4,8×10 ^-4 Вб  определяется законом полного тока

IW= H₁×l₁+ H₂×l₂+H_В×l_В = 1,15×20 + 4,65×40 + 0,96×10⁴×0,12 = 1241 А, что  меньше заданного значения    IW= 5×500 = 2500 А.

Для второго шага приближения необходимо увеличить значение В₂.

Результаты расчётов на каждом шаге сведём в табл. 2.22. Методом линейной интерполяции интервала двух последних шагов получаем значение В₂  для заданной МДС  F = 2500 A:   В₂ = В_В = 1,514 Тл, а остальной расчёт отображает последняя колонка приведенной табл. 2.22, данные которой можно принять за результаты окончательного расчёта. При этом относительная погрешность расчёта по намагничивающей силе

d% =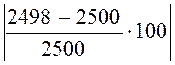= 0,1%.

Таблица 2.22

В2=ВВ, Тл	1,2	1,4	1,5	1,55	1,514
Н2, А/см	4,65	12	22	33	0,508
НВ, ´104 А/см	0,96	1,12	1,2	1,24	1,211
Ф, ´10 –4 Вб	4,8	5,6	6	6,2	6,056
В1, Тл	0,8	0,933	1	1,033	1,01
Н1, А/см	1,15	1,67	2	2,33	2,1
SН×l, А	1241	1875	2360	2855	2498

Запас энергии участка магнитной цепи     W_м=×S×l= ½Ф×U_м.

Для участков цепи:      W_м1 = ½×6,056×10^-4×2,1×20 = 127,2×10 ^-4 Дж;

W_м2 = ½×6,056×10^-4×25,08×40 = 3038×10 ^-4 Дж;