Нелинейные электрические и магнитные цепи постоянного тока, страница 3

I1, А	0	2	4	6	8	10	12
U1, В	0	20	35	46	50	53	54
U– U1= 80 – U1, В	80	60	45	34	30	27	26

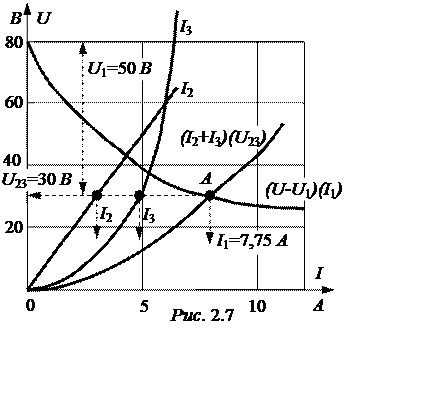Точка А пересечения двух вспомогательных кривых опреде-ляяет решение задачи:  I₁= 7,75 А,    U₂₃= 30 В,   I₂= 3 А,    I₃= 4,75 А,    U₁= 50 В.

Проверка баланса мощнос-тей:   Р_Г = U×I₁ = 80×7,75 = 625 Вт;

SР_П = U₁×I₁ + I₂²×r₂ + U₂₃×I₃ =

= 50×7,75+3²×10+30×4,75 = 620 Вт.

ЗАДАЧА 2.5. Две электри-ческие лампы накаливания с номинальным напряжением 127 В каждая и мощностью 40 и 70 Вт включены последовательно в сеть с напряжением   U = 240 В.  По предварительному расчёту (сопротивления ламп неизменны) напряжения на лампах U₁= 152,5 В, U₂ = 87,5 В.  В действительности вольтамперные характеристики ламп нелинейны и заданы табл. 2.8.

Таблица 2.8

U, В	40	60	80	100	120	140	160	180	200	220
I1, А	0,16	0,2	0,24	0,27	0,3	0,33	0,35	0,38	0,41	0,43
I2, А	0,32	0,38	0,44	0,49	0,54	0,58	0,63	0,68	0,73	0,78

Определить напряжения на лампах.

Ответ:   U₁= 180 В, U₂= 60 В.

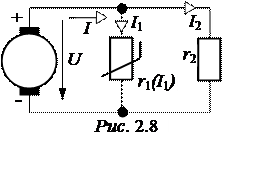
ЗАДАЧА 2.6. Внешняя характеристика генератора постоянного тока (рис.2.8) опреде-ляется данными табл. 2.9.

Таблица 2.9

U, В	220	212	208	204	200	195	188	180	172	160	133
I, А	0	20	30	40	50	60	70	80	90	100	115

Нелинейный элемент r₁(I₁) характеризуется вольтамперной характеристикой табл. 2.10.

Таблица 2.10

U1, В	0	10	25	60	110	180	260
I1, А	0	20	40	60	80	90	95

Сопротивление  r₂ = 6 Ом.   Определить  токи  во всех ветвях схемы рис. 2.8.

Ответы: I₁ = 86 А,   I₂ = 24 А,   I = 110 А.

ЗАДАЧА 2.7. На рис. 2.9,а изображена схема с тремя одинаковыми нелинейными элементами, вольтамперные характеристики которых заданы табл. 2.11. ЭДС источников напряжения   Е₁ = 100 В,   Е₂ = 10 В,   Е₃ = 20 В. Определить токи во всех ветвях схемы, пренебрегая внутренними сопротивлениями источников.

Таблица 2.11

±U, В	0	5	20	30	50	70	100
±I, мА	0	10	30	39	50	55	60

Решение

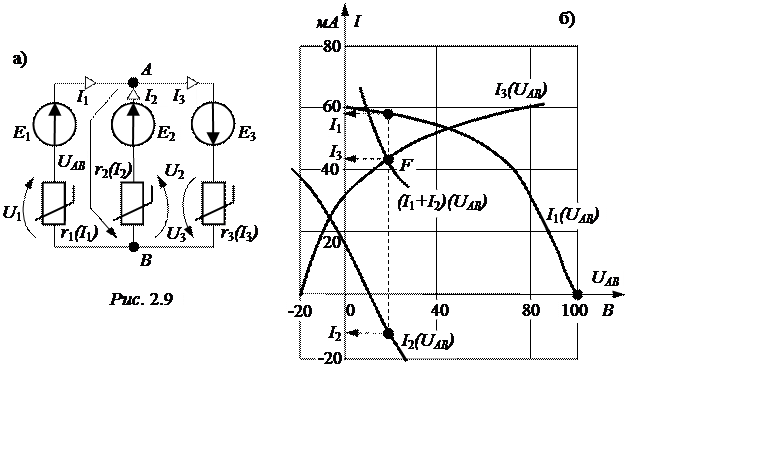
Так как все ветви схемы подключены параллельно к двум узлам схемы А и В, для решения задачи воспользуемся методом узлового напряжения, выбрав произвольные направления токов в ветвях и узлового напряжения U_АВ (указаны на схеме).

Для контуров, в каждый из которых входит U_АВ и одна из ветвей, в соответствии со вторым законом Кирхгофа получаются три уравнения:

U_АВ + U₁ = Е₁,    U_АВ + U₂ = Е₂,    U_АВ – U₃ = -Е₃.

Из этих уравнений выразим U_АВ:

U_АВ = Е₁ – U₁,    U_АВ = Е₂ – U₂,    U_АВ = -Е₃ + U₃.

На основании последних выражений удобно рассчитывается зависимость тока отдельной ветви от узлового напряжения в такой последовательности:

- задаёмся произвольным значением тока ветви в соответствии с вольтамперной характеристикой нелинейного элемента и определяем соответствующее этому значению напряжение нелинейного элемента;

- напряжение U_АВ, при котором в ветви будет выбранное значение тока, рассчитываем по соответствующему уравнению второго закона Кирхгофа.