Нелинейные электрические и магнитные цепи постоянного тока, страница 4

Рассчитанные зависимости   I₁(U_АВ),   I₂(U_АВ),   I₃(U_АВ)   приведены на рис. 2.9,б.

По первому закону Кирхгофа можно записать уравнение    I₁ + I₂ = I₃, которое для рассматриваемой схемы должно выполняться при одном значении U_АВ. Построим вспомогательную кривую (I₁+I₂)(U_АВ) и найдём точку  Fпересечения этой кривой с зависимостью  I₃(U_АВ).

Точка F определяет решение задачи:

U_АВ = 18 В,    I₁ = 58 мА,    I₂ = -15 мА,    I₃ = 43 мА, напряжения на элементахU₁ = 82 В,    U₂ = -8 В,    U₃ = 38 В.   

Алгебраическая сумма мощностей генераторов

SР_Г = Е₁×I₁ + Е₂×I₂ + Е₃×I₃ = 100×58+10×(-15)+20×43 = 6510 мВт;

Сумма мощностей потребителей энергии

SР_П = U₁×I₁ + U₂×I₂ + U₃×I₃ = 82×58 + (-8)×(-15) + 38×43 = 6510 мВт.

Баланс мощностей выполняется.

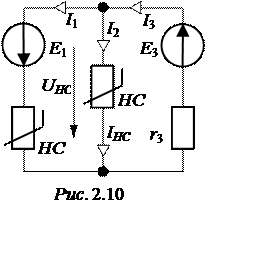
ЗАДАЧА 2.8. В схеме рис. 2.10 определить токи ветвей и проверить баланс мощностей, если  Е₁ = 120 В,   Е₃ = 20 В,  r₃ = 2 кОм, вольтамперная характеристика одинаковых нелинейных сопротивлений (НС) представлена в табл. 2.12.  

Таблица 2.12

UНС, В	5	20	30	50	70	100	150
IНС, мА	10	30	40	50	55	60	65

Ответы: I₁ = 58 мА,   I₂ = -35 мА,

I₃ = 23 мА, SР = 7420 мВт.

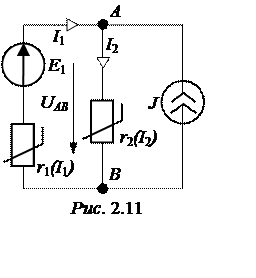
ЗАДАЧА 2.9. Вольтамперные характерис-тики нелинейных элементов r₁(I₁) и r₂(I₂), вклю-ченных в цепь рис. 2.11, приведены в табл. 2.13.

Таблица 2.13

U, В	5	10	20	30	40	50	60	70
I1, А	0,2	0,4	0,68	0,86	0,96	1	1	1
I2, А	1,12	1,4	1,8	2,14	2,44	2,77	3,5	-

Найти токи, проверить баланс мощностей, если  Е₁ = 70 В,   J = 1,5 А.

Ответы: I₁ = 0,9 А,   I₂ = 2,4 А,   U_АВ = 38 В, SР = 120 Вт.

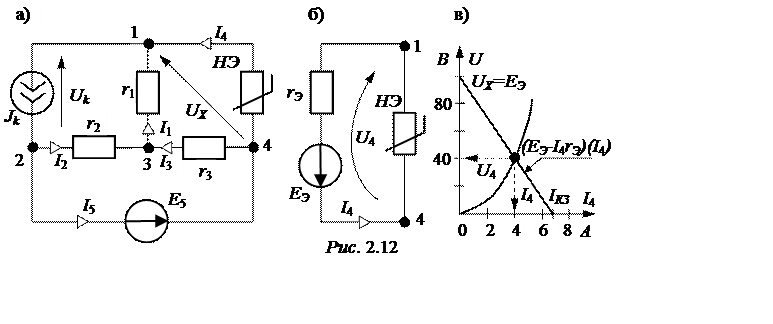
ЗАДАЧА 2.10. На рис. 2.12,а изображена схема с нелинейным элементом (НЭ), вольтамперная характеристика которого задана табл. 2.14.

Таблица 2.14

U4, В	0	20	40	60	80	100
I4, А	0	2,8	4	4,9	5,4	5,7

Параметры линейных элементов  r₁= r₂= r₃= 10 Ом,  Е₅ = 50 В,  J_k = 5 А.  

Определить токи во всех ветвях схемы и проверить баланс мощностей.

Решение

Сначала рассчитаем ток I₄ нелинейного элемента, заменив линейную часть схемы по отношению к зажимам нелинейного элемента (1-4) эквивалентным генератором.

При этом U_Х = Е_Э = I_3Х×r₃ + I_1Х×r₁, где токи с индексом _Х (холостой ход) – это токи элементов схемы, которые получаются после размыкания ветви с нелинейным элементом. В полученной таким образом более простой схеме I_1Х = J_k = 5 А, а по методу контурных токов

I_3Х =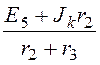==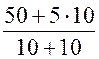 5 А, и  U_Х = 5×10 + 5×10 = 100 В.

Внутреннее сопротивление эквивалентного генератора равно входному сопротивлению пассивной линейной схемы относительно зажимов 1-4:

r_Э = r_14ВХ = r₁ +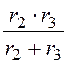 = 10 +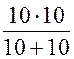= 15 Ом.

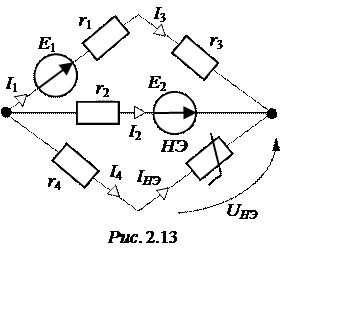
Для эквивалентной схемы (рис. 2.12,б), с одной стороны, U₄(I₄) – ВАХ НЭ, а с другой стороны,  U₄ = Е_Э – I₄×r_Э – ВАХ активного двухполюсника.

Решение системы двух последних уравнений представлено на рис. 2.12,в, откуда   U₄ = 40 В,   I₄= 4 А.

Возвращаемся к исходной схеме рис. 2.12,а и рассчитываем остальные токи:   I₁= J_k - I₄= 5 – 4 = 1 А,

I₃=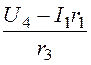==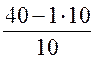 3 А,

I₅= I₃ + I₄ = 3 + 4 = 7 А,

I₂= I₁ – I₃ = 1 - 3 = -2 А, напряжение на зажимах источника тока

U_k = I₂×r₂ + I₁×r₁ = -2×10 +1×10 = -10 В.

Проверка баланса мощностей:

SР_Г = U_k×J_k + Е₅×I₅ = -10×5+50×7 = 300 Вт;

SР_П = I₁²×r₁ + I₂²×r₂ + I₃²×r₃ + U₄×I₄ =

= 1²×10 + 2²×10 + 3²×10 + 40×4 = 300 Вт.

ЗАДАЧА 2.11. В схеме рис. 2.13 рассчитать все токи, если   Е₁ = 4 В,

Е₂ = 16 В,   r₁ = r₂ = r₃ = 2 Ом,   r₄ = 4 Ом, вольтамперная характеристика НЭ представлена табл. 2.15.

Таблица 2.15