Нелинейные электрические и магнитные цепи постоянного тока, страница 6

Примечание: при решении по п.3 и п.4 рекомендуется воспользоваться схемой замещения стабилизатора для отклонений.

Ответы:   I₀ = 414 мА,   h = 76%,   k_ст= ¥. 

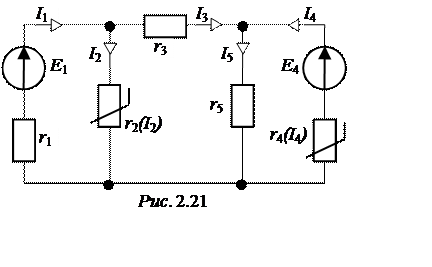
ЗАДАЧА 2.17. В цепи рис. 2.21 кроме линейных сопротивлений

r₁= 2 Ом,   r₃= 1 Ом,   r₅= 2 Ом

имеются ещё два одинаковых нелинейных резистора с заданной вольтамперной характеристикой (табл. 2.18).

Таблица 2.18

U, В	0	1	2	3	4
I, А	0	0,2	0,5	1,0	2,0

ЭДС источников Е₁ = 5 В,   Е₄ = 3 В. Найти токи во всех ветвях схемы.

Примечание: при решении задачи графическим методом рекомендуется одно из параллельных включений сначала заменить эквивалентной ветвью, а затем воспользоваться методом двух узлов.  

Ответы:   I₁ = 1,3 А,   I₂ = 0,7 А,   I₃ = 0,6 А,   I₄ = 0,3 А,   I₅ = 0,9 А.

2.2. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Отличительной чертой расчётов нелинейных магнитных цепей по сравнению с нелинейными электрическими является то, что в исходной задаче расчёта нет необходимых для расчёта вебер-амперных характеристик участков магнитной цепи.

Участок (рис. 2.22,а) характеризуется длиной средней линии магнитопровода l, площадью поперечного сечения сердечника S, кривой намагничивания материала B(H) (рис. 2.22,б), а вебер-амперная характеристика Ф(I) (рис. 2.22,в) рассчитывается.

Магнитная индукция участка   B =, где  Ф[Вб] – магнитный поток,   В[Тл].

Магнитное напряжение на участкеU_мАВ = H×l= Ф×R_м, где  H[А/м] – напряжённость магнитного поля участка,

R_м =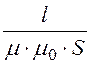 [1/Гн] – магнитное сопротивление участка, соответствую-щее статическому сопротивлению нелинейного резистора в электрической цепи,

m₀ = 4p×10 ^-7 Гн/м – магнитная постоянная,

m– относительная магнитная проницаемость материала участка, нелинейно зависящая от магнитной индукции.

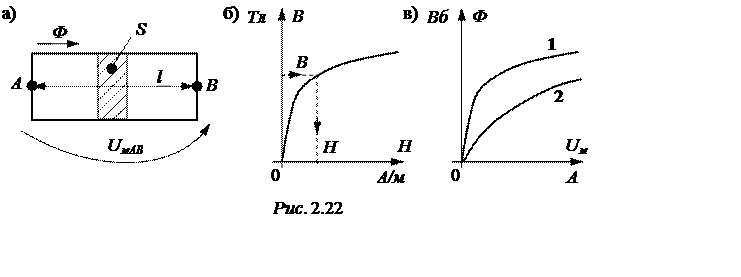
При постоянных потоках зависимость между В и H задаётся кривой намагничивания (рис. 2.22,б) материала сердечника, хотя часто выражается формулой   В = mm₀×H.

Для воздушных зазоров  m= 1  и   В_В = m₀×H.

Обычно расчёт вебер-амперной характеристики ведут в следующей последовательности:

1) задают произвольное значение В,

2) рассчитывают соответствующее значение потока  Ф = В×S,

3) определяется по кривой намагничивания соответствующее принятому В значение H (рис. 2.22,б),

4) находят  U_м = H×l.

Примечание: при наличии воздушного зазора на участке пользуются следующей приближённой формулой:

Н_В == 0,8×10⁶×В_В, где    H_В[А/м],  В_В[Тл=Вб/м²].

Тогда   U_мАВ = H×l + H_В×l_В.

Расчёты повторяют для диапазона изменений индукции от нуля до 1,5¸1,7 Тл, сводят их в таблицы и строят вебер-амперные характеристики (рис. 2.22,в), где  1 – ВбАХ при отсутствии воздушного зазора на участке,

2 – ВбАХ при наличии воздушного зазора.

В дальнейшем методика расчёта магнитных цепей совпадает с методикой расчёта нелинейных электрических цепей и для наглядности расчётов можно составлять эквивалентную расчётную схему – аналог электрической цепи.

ЗАДАЧА 2.18. На рис. 2.23,а представлен дроссель, являющийся катушкой с числом витков W= 500, намотанной на сердечник из электротехнической стали 1512, кривая намагничивания которой приведена в табл. 2.19.  Длина средней линии магнитопровода  l= 100 см,  сечение стали S= 16 см². Воздушный зазор отсутствует  l_В = 0.  Рассчитать и построить вебер-амперную характеристику катушки.

Таблица 2.19

Кривая намагничивания стали 1512

В, Тл	0,2	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1
Н, А/см	0,25	0,5	0,65	0,8	0,95	1,15	1,5	2	3

Продолжение таблицы 2.19

В, Тл	1,2	1,3	1,35	1,4	1,45	1,5	1,55	1,6	1,65
Н, А/см	4,65	7,4	9	12	15	22	33	49	90