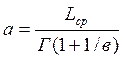 (9)
(9)
где
![]() - гамма – функция по аргументу
- гамма – функция по аргументу ![]() , который берется из табл.4 приложение 4 в
зависимости от коэффициента вариации V.
Чтобы найти, гамма – функцию
, который берется из табл.4 приложение 4 в
зависимости от коэффициента вариации V.
Чтобы найти, гамма – функцию![]() пользуемся тем же
алгоритмом как находили параметр формы b закона Вейбулла-Гнеденко.
пользуемся тем же
алгоритмом как находили параметр формы b закона Вейбулла-Гнеденко.
Число 0,33 Из табл.4 берем, тогда получим:
![]()
Подставляя значения, получим:
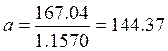
Граничные значения интервальной оценки, тыс.км:
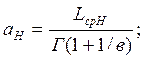 (10)
(10)
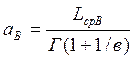 (11)
(11)
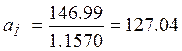
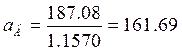
Прежде чем перейти к оценке остальных показателей надежности, необходимо проверить принятую в п.1 нулевую гипотезу о соответствии экспериментального распределения отказов распределению Вейбулла-Гнеденко.
Соответствие закона Вейбулла-Гнеденко экспериментальному распределению
проверяем по ![]() - распределения согласия Пирсона. Нет оснований
для отклонения нулевой гипотезы при соблюдении условия:
- распределения согласия Пирсона. Нет оснований
для отклонения нулевой гипотезы при соблюдении условия:
![]()
где
![]() - значение критерия, вычисленное по
экспериментальным данным;
- значение критерия, вычисленное по
экспериментальным данным; ![]() - критическая точка
(табличное значение) критерия при уровне значимости
- критическая точка
(табличное значение) критерия при уровне значимости ![]() и числе
степени свободы k.(Берем из табл. 2 приложение 2).
и числе
степени свободы k.(Берем из табл. 2 приложение 2).
Уровень
значимости ![]() примем равным 0,1.
примем равным 0,1.
Число степеней свободы:
![]() (12)
(12)
где
S – количество частичных интервалов выборки; r – количество параметров
предполагаемого распределения. При двухпараметрическом законе Вейбулла-Гнеденко
![]() .
.
Нулевая гипотеза проверяется по следующему алгоритму:
5 Количество интервалов S по правилу Штюргеса с округлением до целого значение
![]() (13)
(13)
Получаем:
![]()
Тогда:
![]()
Табличное
значение критерия ![]() .
.
Затем определяют длину интервала как отношение размаха вариационного ряда на число интервалов т.е. разность между наибольшим и наименьшим значениями вариационного ряда:
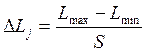 (14)
(14)
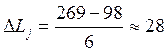
Границы интервалов определим по формуле:
![]() (15)
(15)
где j=1, 2, …, s.
![]()
![]()
![]()
![]()
![]()
![]()
6 Теоретические частоты
![]() (16)
(16)
где j = 1, 2, …, S.
или:
![]() ,
(17)
,
(17)
Функцию распределения отказов определяют по формуле(для закона Вейбулла-Гнеденко):
![]() (18)
(18)
где: L – средняя наработка на отказ (тыс.км) ;а-точная оценка параметра закона Вейбулла – Гнеденко в тыс. км.
![]()
![]()
![]()
![]()
![]()
![]()
Теперь
рассчитаем ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Значит
![]() равно:
равно:
![]()
![]()
![]()
![]()
![]()
![]()
Результаты расчета занесем в таблицу 1.
Таблица
1 - Расчет ![]() - распределения согласия Пирсона
- распределения согласия Пирсона
|
j |
Lj-1 |
Lj+1 |
nj |
nj² |
∆F(Lj) |
n¯j |
nj²/n¯j |
||||||
|
1 |
0 |
126 |
7 |
49 |
0,2295 |
5.2888 |
9.2647 |
||||||
|
2 |
126 |
154 |
5 |
25 |
0.1772 |
4.0767 |
6.1323 |
||||||
|
3 |
154 |
182 |
4 |
16 |
0,1988 |
4.5740 |
3.4980 |
||||||
|
4 |
182 |
210 |
1 |
1 |
0.1769 |
4.0691 |
3.2457 |
||||||
|
5 |
210 |
238 |
3 |
9 |
0,1211 |
2.8085 |
3.2045 |
||||||
|
6 |
238 |
269 |
3 |
9 |
0,0674 |
1.5515 |
3.1005 |
||||||
|
Σnj= |
Σ= |
Σ= |
1 |
n¯j= |
23 |
Σ= |
28.44 |
||||||
2.4.3 Определение расчетного значения критерия
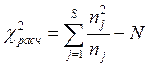 (21)
(21)
![]()
В
результате получаем ![]() <
<![]() . Так
как условия выполнения нулевой гипотезы соблюдаются, то гипотеза о нормальном
распределении принимается.
. Так
как условия выполнения нулевой гипотезы соблюдаются, то гипотеза о нормальном
распределении принимается.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.