Построение многоугольников и многогранников

6. ПОСТРОЕНИЕ МНОГОУГОЛЬНИКОВ И МНОГОГРАННИКОВ

Данная глава посвящена алгоритмам построения звездчатых и выпуклых геометрических фигур. Показано, как эти алгоритмы применяются для разработки конструкторов классов многоугольников и многогранников соответствующих типов.

Сначала изучаются тесты на принадлежность точки многоугольнику. Затем рассматриваются методы построения звездчатых многоугольников, выпуклых многоугольников и многогранников. Описываются различные алгоритмы построения выпуклых оболочек. Предлагаются программные реализации этих методов.

6.1. ТЕСТЫ ПРИНАДЛЕЖНОСТИ ТОЧКИ МНОГОУГОЛЬНИКУ

Будем рассматривать многоугольники, заданные как лежащие в декартовой плоскости  замкнутые ломаные, состоящие из отрезков p₀p₁, p₁p₂,…,p_n-1p₀. Каждый многоугольник определен последовательностью точек (p₀, p₁,…,p_n-1), которые являются его вершинами. Сформулируем основную задачу данного параграфа.

Даны многоугольник P, вершинами которого служат точки (p₀, p₁,…,p_n-1), и точка t. Определить, находится ли точка t внутри многоугольника P.

Рассмотрим эту задачу сначала для простого многоугольника — многоугольника, у которого никакая пара непоследовательных ребер не имеет общих точек. Например, любой выпуклый многоугольник является простым. Отметим, что многоугольник, приведенный на рис. 6.1, является простым.

Согласно теореме Жордана, простой многоугольник разбивает плоскость на две части — внутреннюю и внешнюю. Если точка t имеет координаты (x_t, y_t), то проведем от нее горизонтальный луч, состоящий из точек (x, y), таких, что x > x_t и y = y_t. Согласно стандарту GKS, точка t называется внутренней, если число точек пересечения луча со сторонами многоугольника нечетно. В противном случае она называется внешней.

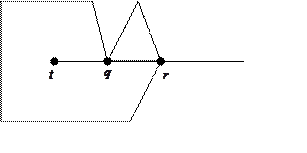Рис. 6.1. Пример расположения точки и многоугольника

В этом примере луч пересекается с границей многоугольника в четном числе точек, хотя точка является внутренней. Если же подсчитывать число пересечений луча со сторонами многоугольника, то точка q и точка r будут учитываться дважды, и вновь получаем четное число пересечений со сторонами многоугольника.

Анализ этого примера приводит к выводу, что точку q следует учитывать два раза или не учитывать совсем, а точку r — один раз. Следовательно, при определении, пересекаются ли горизонтальный луч и отрезок, мы не должны учитывать точки отрезка, имеющие максимальную ординату.

В примере (рис. 6.1) получаем, что число точек пересечения со сторонами равно 1 + 1 + 1 + 0.

Алгоритм проверки на принадлежность точки t многоугольнику p₀, p₁,…,p_n-1 будет состоять из следующих действий:

1.  Установить четность parity = 0.

2.  Организовать цикл по i = 0, 1, 2,…,n-1, в теле которого, в случае, когда пересечение луча, проведенного вправо от точки t, с отрезком p_ip_(i+1)%n не пусто, применяется операция изменения четности parity = 1 – parity.

3.  После окончания работы цикла, если parity = 1, то точка расположена внутри, а в случае parity = 0 — снаружи многоугольника.

При программной реализации проверка на пересечение луча и отрезка будет осуществляться в подпрограмме (функции), возвращающей 1, если пересечение не пусто, и 0 — в противном случае. Если общей точкой луча и отрезка является точка отрезка с максимальной ординатой, то возвращается 0. В частности, пересечение луча с горизонтальным отрезком всегда считается пустым. Луч, исходящий из точки (x, y), будет пересекаться с отрезком, соединяющим точки (x₁, y₁) и (x₂, y₂), если min (y₁, y₂) ≤ y < max (y₁, y₂) и, более того, точка пересечения горизонтальной прямой с отрезком находится справа от точки (x, y).

Для реализации алгоритма определим класс точки как структуру, состоящую из координат. Разработаем с помощью этой структуры подпрограмму проверки на пересечение горизонтального луча с отрезком и определим многоугольник как класс, состоящий из массива вершин многоугольника и теста на принадлежность точки многоугольнику.

struct Point

{

float x, y;                        // координаты точки

};

int intersect(Point p, Point p1, Point p2)

{

// проверка пересечения луча с отрезком

if(p1.y == p2.y) return 0;

if((p1.y < p2.y ? p2.y:p1.y) <= p.y) return 0;  // max(y1,y2)<=y

if((p1.y < p2.y ? p1.y:p2.y) > p.y) return 0;   // min(y1,y2)>y

if(p2.y - p1.y>0)     // если y2>y1, то векторное произведение > 0

return ((p.x - p1.x) * (p2.y - p1.y) –

(p2.x - p1.x) * (p.y - p1.y) > 0);

else

return ((p.x - p1.x) * (p2.y - p1.y) –

(p2.x - p1.x) * (p.y - p1.y) < 0);

}

class Polygon

{

int n;                             // количество вершин