Построение многоугольников и многогранников, страница 13

{

int i, i1, i2, i3;

Pnt3 p[4], temp;

float v, volume=0.;

ff=NULL;

for (i=0;i<n;i++)

for (i1=i+1;i1<n;i1++)

for (i2=i1+1;i2<n;i2++)

for (i3=i2+1;i3<n;i3++)

{

v=vol(pt[i],pt[i1],pt[i2],pt[i3]);

if(fabs(v)>fabs(volume))

{

volume = v;

p[0]=pt[i];p[1]=pt[i1];p[2]=pt[i2]; p[3]=pt[i3];

}

}

if (fabs(volume)<0.00001)

{

Form1->Image1->Canvas->TextOutA(10,10, "Complanar Points"); return;

} else

{

if(volume>0)

{                                // инверсия

temp=p[3]; p[3]=p[0]; p[0]=temp;

temp=p[2]; p[2]=p[1]; p[1]=temp;

}

append(p[1],p[2],p[3]);

append(p[0],p[3],p[2]);

append(p[0],p[1],p[3]);

append(p[0],p[2],p[1]);

}

for (i=0; i<n; i++) addpnt(pt[i]);

}

convex cb;

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

d=100; zv=d/2.5;

cosa=1; sina=sqrt(1-cosa*cosa);

xv=d*cosa; yv=d*sina;

maxX = Form1->Image1->Width;

maxY = Form1->Image1->Height;

pxmax=d/2; pxmin=-d/2;

pymax=0.;

pymin=-(pxmax-pxmin)*maxY/maxX;

Bitmap = new Graphics::TBitmap;

Bitmap->Width=maxX;

Bitmap->Height=maxY;

/*

convex cv(o, radius*e1, radius*e2, radius*e3);

cv.addpnt(radius*(e1+e2+e3));

cv.addpnt(radius*(e1+e2));

cv.addpnt(radius*(e2+e3));

cv.addpnt(radius*(e1+e3));

cv.addpnt(12.5*e1+37.5*e3);

cv.addpnt(12.5*e1+25*e2+37.5*e3);

*/

Pnt3 p[10];

p[0]=o; p[1]=radius*e1; p[2]= radius*e2; p[3]= radius*e3;

p[4]=radius*(e1+e2+e3);

p[5]=radius*(e1+e2);

p[6]= radius*(e2+e3);

p[7]= radius*(e1+e3);

p[8]= 0.5*radius*e1+1.5*radius*e3;

p[9]= 0.5*radius*e1+radius*e2+1.5*radius*e3;

convex cv(p, 10);

cb=cv;

Timer1->Interval=200;

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

Timer1->Enabled=!Timer1->Enabled;

}

//--------------------------------------------------------------------------void __fastcall TForm1::Timer1Timer(TObject *Sender)

{

static int i;

cosa=cos(0.1*i); sina=sin(0.1*i); i++;

xv=d*cosa; yv=d*sina;

cb.display();

}

//--------------------------------------------------------------------------Результаты работы программы приведены на рис. 6.10.

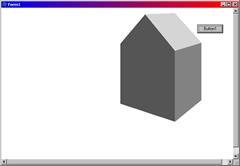
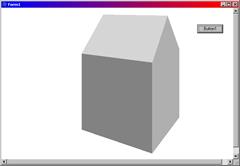
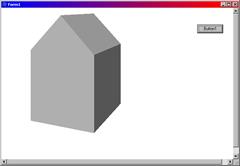
Рис. 6.10. Вращение выпуклой оболочки вокруг вертикальной оси

6.4. МЕТОДЫ ПОСТРОЕНИЯ ВЫПУКЛОЙ ОБОЛОЧКИ

Рассмотрим алгоритмы построения выпуклой оболочки множества точек в плоскости.

Метод заворачивания подарка. Этот метод построения выпуклой оболочки основан на том, что отрезок, соединяющий две точки заданного конечного множества, является ребром выпуклой оболочки тогда и только тогда, когда все другие точки заданного множества расположены на этом отрезке или с одной стороны от него. Отметим, что если отрезок ab, соединяющий точки a и b, является ребром выпуклой оболочки, то существует еще одно ребро, с вершиной в точке b.

Пусть задано конечное множество точек плоскости. Обозначим это множество M. Предположим, что выбрана точка (x_a, y_a), которая заведомо является одной из вершин выпуклой оболочки. Для этого годится точка, имеющая наименьшую абсциссу. Если таких точек несколько, то выбираем среди них точку с наименьшей ординатой. Вокруг этой точки поворачивается исходящий из нее луч по направлению движения часовой стрелки до тех пор, пока он не встретит некоторую точку (x_b y_b) из множества M. Отрезок, соединяющий точку (x_a, y_a) с точкой (x_b, y_b), будет стороной строящегося выпуклого многоугольника (рис. 6.11).

Для поиска следующего ребра продолжим вращение луча по часовой стрелке. На этот раз луч будет вращаться вокруг точки b до встречи со следующей точкой c, принадлежащей множеству M. Затем луч вращается вокруг точки c  M до встречи с новой точкой d, как это показано на рис. 6.11. Процесс продолжается до тех пор, пока не будет достигнута точка a. На рис. 6.11 показан пример построения выпуклой оболочки, в результате которого будет получен многоугольник abcde.

Рис. 6.11. Метод заворачивания подарка