Построение многоугольников и многогранников, страница 6

Построение выпуклой оболочки на плоскости. Алгоритм Дейкстры строит выпуклый многоугольник по шагам. Сначала берется тройка точек. Она составляет начальный выпуклый многоугольник. Затем последовательно присоединяются остальные точки. При каждом присоединении многоугольник достраивается до выпуклого многоугольника, содержащего очередную точку, описанным далее образом.

Напомним, что точка q многоугольника называется видимой из точки p, не принадлежащей многоугольнику, если отрезок pq не содержит точек многоугольника, кроме точки q. Сторона многоугольника называется видимой из точки p, если она состоит из видимых точек. Пусть P — наименьший выпуклый многоугольник, содержащий первые k точек входного массива, p — (k + 1)-я точка. Если p принадлежит многоугольнику P, то многоугольник P не изменится. В противном случае (рис. 6.6) удаляются видимые стороны многоугольника P и добавляются две стороны, которые являются прямолинейными отрезками, соединяющими точку p с двумя крайними точками оставшихся сторон.

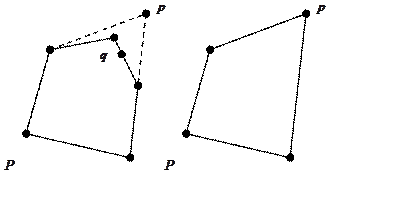Рис. 6.6. Добавление точки p к многоугольнику P

Последовательно добавляя точки входного массива, получим выпуклую оболочку этих точек.

Для программной реализации этого метода построения выпуклой оболочки определим класс выпуклого многоугольника как производный от класса звездчатого многоугольника. Разработаем составную функцию добавления точки. Конструктор будет строить выпуклый многоугольник, многократно обращаясь к функции добавления (предполагается, что закрытые члены класса SPolygon заменены на защищенные).

class CPolygon:public SPolygon

{

public:

void Insert(Point t)          // добавление точки

{

int i; int j;

if(isin(t)) return;      // t принадлежит

int *del = new int [n];  // n – число вершин

Point *q = new Point [n + 1];  // формируемый

// многоугольник

j0 = j1 = 0;

for(i = 0; i < n; i++)

{

if((t - p[i]) * (p[(i + 1)%n] - p[i]) >= 0)

del[i] = 1;   // отмечаем видимые стороны

else del[i] = 0;

}

for(i = 0; i < n; i++)

if(del[i] == 1 && del[(I + 1)%n] == 0) break;

j = 0; i = (i + 1)%n;    // i – номер последней

// невидимой стороны

while(del[i] == 0)

{

q[j++] = p[i]; i = (i + 1)%n;    // перепись вершин

}

q[j] = p[i];

q[j + 1] = t;                  // добавление вершин

delete []p;

delete []del;

p = new Point [j + 2]; n = j + 2;

for(i = 0; i < n; i++)

p[i] = q[i];

delete []q;

}

CPolygon(float *x, float *y, int m, int cl);

};

// Конструктор

CPolygon::CPolygon(float *x, float *y, int m, int cl):color(cl)

{

// выпуклая точка массива точек (x[i], y[i])

int i; Point t;

p = new Point [3]; n = 3;          // начальный треугольник

for(i = 0; i < 3; i++)

{

p[i].x = x[i]; p[i].y = y[i];

}

if((p[1] - p[0]) * (p[2] - p[1]) <0 )

{

// ориентация против часовой стрелки

t = p[1]; p[1] = p[2]; p[2] = t;

}

for(i = 3; i < m; i++)

{

t.x = x[i]; t.y = y[i];

Insert(t);                    // добавление точки

}

}

Предполагается, что первые три точки не лежат на одной прямой.

Приведем полный текст программы, в которой строится выпуклая оболочка методом Дейкстры. Тест на принадлежность точки многоугольнику реализуется с помощью метода горизонтального луча.

//--------------------------------------------------------------------------#include <vcl.h>

#pragma hdrstop

#include "Unit1.h"

//--------------------------------------------------------------------------#pragma package(smart_init)

#pragma resource "*.dfm"

#include <math.h>

#include <stdlib.h>

#define PI 3.14159

TForm1 *Form1;

int getmaxx()

{

return Form1->Image1->Width;

}

int getmaxy()

{

return Form1->Image1->Height;

}

void line(int x0, int y0, int x1, int y1)

{

Form1->Image1->Canvas->MoveTo(x0,y0);

Form1->Image1->Canvas->LineTo(x1,y1);

}