Построение многоугольников и многогранников, страница 5

float xmin, ymin, xmax, ymax;      // окно

public:

Wnd(float x0, float y0, float x1, float y1):

xmin(x0), ymin(y0), xmax(x1), ymax(y1){}

Wnd& operator<<(SPolygon);

Wnd& operator<<(Pnt);

};

Wnd& Wnd::operator<<(SPolygon f)

// операция вывода многоугольника в окно

{

int i;

TPoint *parray = new TPoint [f.n];

Form1->Image1->Canvas->Brush->Color=f.color;      // цвет точек многоугольника

for(i = 0; i < f.n; i++)

{

parray[i] = Point(

((f.p[i]).x - xmin)*(Form1->Image1->Width) / (xmax - xmin),

(ymax - (f.p[i]).y) *(Form1->Image1->Height) / (ymax - ymin));

}

Form1->Image1->Canvas->Polygon(parray, f.n-1);

// вывод с помощью стандартной функции

return *this;

}

Wnd& Wnd::operator<<(Pnt t)

{

Form1->Image1->Canvas->Pixels

[(t.x - xmin) * (Form1->Image1->Width) / (xmax - xmin)]

[(ymax - t.y) * (Form1->Image1->Height) / (ymax - ymin)]=clBlack;

return *this;

}

//--------------------------------------------------------------------------__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

// главная программа

Wnd w(-300, -300, 300, 300);

float rad = 300, xx[10], yy[10];            // радиус и координаты

int i; Pnt t;                                 // счетчик и точка

for(i = 0; i < 5; i++)

{

xx[i] = rad * cos(2 * PI * i / 5);    // берутся точки на

yy[i] = rad * sin(2 * PI * i / 5);    // окружности радиуса rad

xx[i + 5] = rad * cos(2 * PI * i / 5 + PI / 5) / 2;// и на окружности

yy[i + 5] = rad * sin(2 * PI * i / 5 + PI / 5) / 2;// радиуса rad/2

}

SPolygon sp(xx,yy,10,(TColor)RGB(0,255,100));     // объект - многоугольник

w<<sp;                             // вывод многоугольника на экран

float sx, sy;                             // проверка теста на принадлежность

for(sx = -300; sx <= 300; sx += 5) // пробегаются все

{

for(sy = -300; sy <= 300; sy += 5)// точки окна

{

t.x = sx; t.y = sy;       // если точка не принадлежит

if(sp.isin(t) == 0) w<<t; // окну, то выводится на экран

}

}

}

//--------------------------------------------------------------------------Результаты работы программы показаны на рис. 6.5. Поскольку при выполнении операции w<<sp вывода многоугольника sp в окно w объект sp передается по значению, вызывается конструктор копирования объекта sp.Если не определить конструктор копирования явно, то будет выполняться побитное копирование указателя на массив точек. При выходе из подпрограммы, выполняющей операцию w<<sp, будет освобождаться область, адресом которой является этот указатель, и массив точек может измениться. Для того чтобы исключить эту возможность, мы определили явно конструктор копирования Spolygon(const SPolygon &ob).

Рис. 6.5. Звездчатый многоугольник

Отметим, что текст программы начинается с определения класса окна Wnd, в котором для вывода многоугольника переопределяется операция <<. Затем определяется структура точки и операции, необходимые для построения звездчатого многоугольника. Также определяется класс, объектами которого являются звездчатые многоугольники, и составная функция этого класса, реализующая тест на принадлежность методом углов.

6.3. ПОСТРОЕНИЕ И ИЗОБРАЖЕНИЕ ВЫПУКЛОЙ ОБОЛОЧКИ

Выпуклой оболочкой множества точек называется наименьшее выпуклое множество, содержащее эти точки. Выпуклая оболочка множества точек {p₀, p₁,…, p_n–1} будет состоять из всех точек p, для которых существуют неотрицательные действительные числа t_i ≥ 0, 1 ≤ i ≤ n, такие, что 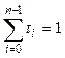 и p = t₀p₀ + t₁p₁ +…+t_n-1p_n-1 (здесь точки p_i рассматриваются как радиус-векторы). Например, выпуклой оболочкой двух точек будет соединяющий их прямолинейный отрезок. Выпуклой оболочкой не лежащих на одной прямой трех точек будет треугольник, вершинами которого являются эти точки.