Построение многоугольников и многогранников, страница 10

1.  Преобразовать координаты вершин в проекционные координаты.

2.  Для каждой грани k, 1 ≤ k ≤ K, найти уравнение плоскости a_kX + b_kY + c_kZ + d_k = 0, проходящей через точки граней. Это можно сделать, например, с помощью формул усреднения Мартина-Ньюэла, позволяющих записать уравнение плоскости, проходящей через точки (X_i, Y_i, Z_i), при 0 ≤ i < n, где j зависит от i следующим образом: j = (i + 1) mod n.

,,.

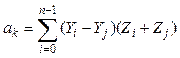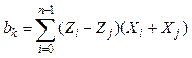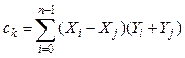Коэффициент d_k вычисляется с помощью любой точки плоскости (X₀, Y₀, Z₀), а именно: d_k = – a_kX₀ – b_kY₀ – c_kZ₀.

3.  Вычислить значения линейных функций a_kX + b_kY + c_kZ + d_k  в центре тяжести вершин тела. Если значение k-й функции в центре тяжести больше 0, то изменить коэффициенты  на противоположные: a_k = – a_k, b_k = – b_k, c_k = – c_k, d_k = – d_k.. Координаты центра тяжести тела можно найти как среднее арифметическое координат всех вершин этого тела.

4.  Вычислить коэффициенты c_k. Если c_k > 0, то вывести (или установить признак видимости) грань с номером k.

Такой подход можно применить и в случае центральной проекции. Но центральная проекция не переводит плоскость в плоскость, если учитывать третью координату, что мешает нахождению проекционных координат точек грани по проекционным координатам вершин этой грани, необходимому во многих алгоритмах реалистичного изображения тел.

Для нахождения видимых граней в центральной проекции сначала находятся уравнения плоскостей в мировых координатах (x, y, z), содержащих грани. Пусть f_k (x, y, z) = a_kx + b_ky + c_kz + d_k = 0 — уравнение k-й грани. Если значение f_k (x, y, z) в центре тяжести больше нуля, то следует изменить коэффициенты на противоположные. После этого вектор (a_k, b_k, c_k) будет вектором внешней нормали. Далее берется произвольная точка p, принадлежащая k-й грани, и соединяется с точкой q_V, в которой находится наблюдатель. Если угол между вектором внешней нормали (a_k, b_k, c_k) и вектором  является острым, то грань будет видимой, и эту грань следует вывести на экран. В противном случае k-я грань невидима. Для каждой грани расчеты и вывод на экран выполняются независимо друг от друга.

Программа пострения выпуклой оболочки в трехмерном пространстве. Определим класс выпуклого тела. Конструктор строит выпуклое тело по четырем некомпланарным точкам. Выпуклая оболочка получается добавлением остальных точек к этому телу. Точка обзора перемещается по окружности, находящейся на высоте z_V. Это позволяет увидеть созданное выпуклое тело с различных сторон. Определим структуры данных для разработки приложения.

q  class Pnt3 — класс, объектами которого являются точки трехмерного пространства. Над соответствующими этим точкам радиус-векторами определим векторные операции. В частности, точки

Pnt3 o(0, 0, 0), e1(1, 0, 0), e2(0, 1, 0), e3(0, 0, 1);

задают начало координат и базис.

q  Двухсвязный список ребер, структура элемента которого определена как

struct edge

{

Pnt3 p0, p1;

struct edge *prev, *next;

}

вместе с функциями добавления и удаления элемента списка. Помимо этих функций определим функцию, имеющую прототип

edge *xoredge(edge *first, Pnt3 q0, Pnt3 q1);

добавляющая в список ребро, соединяющее точки q0 и q1, если такого ребра в списке нет.

Если в списке есть ребро с началом q1 и концом q0, то оно удаляется. В этом случае ребро, соединяющее точки q0 и q1, не добавляется.

q  Класс выпуклого тела определяется как список треугольных граней

class convex

{

face *ff;

public:

void append(Pnt3 pt0, Pnt3 pt1, Pnt3 pt2);

void delface(face *cur);

int addpnt(Pnt3 v);

void display();