Построение многоугольников и многогранников, страница 18

(int)((300. - y[i]) * getmaxy() / 600 - 1),

(int)((x[i] + 300.) * getmaxx() / 600) + 1,

(int)((300. - y[i]) * getmaxy() / 600) + 1);

}

delete []x; delete []y;

}

//--------------------------------------------------------------------------Программа выводит случайные точки и их выпуклые оболочки. Результат работы программы приведен на рис. 6.14.

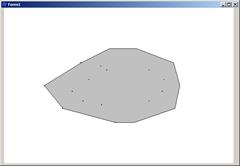
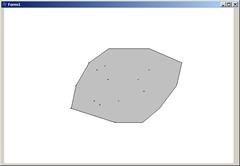
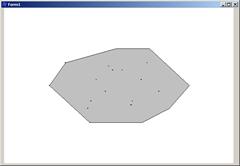
Рис. 6.14. Выпуклые оболочки, построенные методом Грэхема

Для создания проекта необходимо выполнить следующие действия:

1.  Перенести компонент Image, со страницы Additional на главную форму Form1.

2.  Перенести компонент Button со страницы Standartнаглавную форму Form1.

3.  Щелкнув дважды курсором мыши на кнопке Button, набрать приведенный выше текст модуля Unit1.cpp.

4.  Запустить проект на компиляцию, сборку и выполнение, выбрав пункт Run главного меню.

Метод Эндрю. В методе обхода Грэхема имеется один недостаток: при упорядочении точек используется сравнение углов. Чтобы исправить этот недостаток, Эндрю предложил следующую модификацию метода обхода Грэхема, в которой вместо сравнения углов применяется сравнение абсцисс точек.

Пусть задано конечное множество M точек плоскости, состоящее из m элементов. Сначала находятся его левая крайняя точка l и правая крайняя точка r этого множества. Для определенности среди точек с наименьшей абсциссой выбирается точка с наименьшей ординатой, а среди точек с наибольшей абсциссой — точка с наибольшей ординатой. Построим прямую, проходящую через точки l и r (рис. 6.15). Множество M разбивается на два подмножества, первое из которых состоит из точек, расположенных выше прямой, и называется верхним подмножеством, а второе состоит из остальных точек и называется нижним подмножеством.

Рис. 6.15. Разбиение, определенное крайними точками

Строится выпуклая оболочка верхнего подмножества вместе с точками l и r. Затем строится выпуклая оболочка нижнего подмножества и точек l и r. В результате получаем две ломанные, которые вместе составляют выпуклый многоугольник, ограничивающий искомую выпуклую оболочку.

Выпуклая оболочка верхнего подмножества и точек l и r строится в два этапа:

1.  Верхние точки вместе с точками l и r сортируются по возрастанию абсцисс. Среди точек с одинаковой абсциссой оставляется лишь верхняя.

2.  Производится просмотр троек p_ip_i+1p_i+2 верхних точек. Если вектор p_ip_i+1 расположен слева от p_ip_i+2, то увеличивается i, в противном случае точка p_i+1 удаляется из списка (или массива) верхних точек.

Результат работы программы приведен на рис. 6.16.

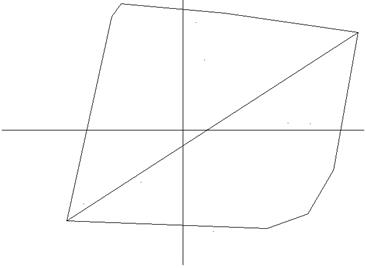Рис. 6.16. Выпуклая оболочка, построенная методом Эндрю

6.5. ЗАДАЧИ

1.  Пусть P — простой многоугольник с n вершинами (x_i, y_i),0 ≤ i < n. Доказать, что его площадь равна абсолютной величине суммы 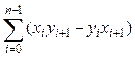, где индексы i+1 берутся по модулю n , т. е. x_n = x₀ и y_n = y₀.

2.  Написать подпрограмму, находящую пересечение двух выпуклых многоугольников, лежащих в декартовой плоскости и заданных координатами вершин.

Указание. Применить алгоритм Шеймоса-Хоея. Через вершины заданных многоугольников провести горизонтальные прямые. В результате вся плоскость будет разбита на горизонтальные полосы, а каждый из многоугольников будет разбит на трапеции и треугольники. Эти полосы просматриваются сверху вниз, и в каждой полосе вычисляется пересечение соответствующих трапеций (см. [11]).

3.  (Триангуляция простого многоугольника.) Многоугольник, заданный вершинами (P₀ ,P₁ ,…,P_n-1 ) называется простым, если его стороны, кроме соседних, не имеют общих точек. Триангуляцией многоугольника называется его разбиение на треугольники, вершины которых принадлежат множеству {P₀ , P₁ , … , P_n-1 }. Разработать алгоритм и написать программу, строящую триангуляцию простого многоугольника.