Построение многоугольников и многогранников, страница 3

q = p[i];

}

ind = ind / 4;

if(ind == 0) return 0;

else return 1;

}

Чтобы эта функция работала, необходимо дополнить класс точки функцией вычисления кода и операциями разности и векторного произведения для плоских векторов. Под векторным произведением плоских векторов v * w подразумевается число, равное |v| · |w| · sinα, где α – угол между векторами v и w. Учитывая эти дополнения, получим структуру точки:

struct Point

{

float x, y;                  // координаты точки

int code(Point q);           // код четверти точки q в предположении,

// что (x,y) – начало координат

float operator*(Point q);          // векторное произведение

Point operator-(Point q);          // разность векторов

};

int Point::code(Point q)

{

if(q.x – x >= 0 && q.y – y >= 0) return 0;

if(q.x – x < 0 && q.y – y >= 0) return 1;

if(q.x – x >= 0 && q.y – y < 0) return 3;

if(q.x – x < 0 && q.y – y < 0) return 2;

}

Point Point::operator-(Point q)          // разность

{

Point t;

t.x = x - q.x; t.y = y - q.y;

return t;

}

float Point::operator*(Point q)

{

return x * q.y – y * q.x;          // векторное произведение

}

6.2. ПОСТРОЕНИЕ ЗВЕЗДЧАТОГО МНОГОУГОЛЬНИКА

Дадим определение звездчатого многоугольника. Пусть точки p и q принадлежат некоторому многоугольнику P, т.е. расположены внутри многоугольника или на его границе. Будем говорить, что точка q видна из точки p, если прямолинейный отрезок pq состоит из точек, принадлежащих многоугольнику P.

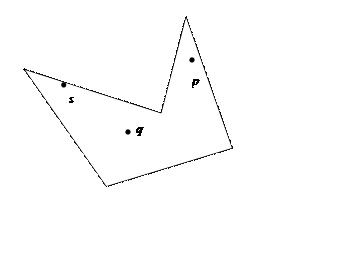Рис. 6.4. Видимость точек

Например, на рис. 6.4 точка q видна из точки s, а точка p не видна из точки s. Множество точек многоугольника, из которых видны все точки этого многоугольника, называется ядром многоугольника. Отметим, что ядро выпуклого многоугольника составляют все его точки. Многоугольник называется звездчатым, если его ядро не пустое. Заметим, что ядро звездчатого многоугольника всегда является выпуклым множеством.

Опишем алгоритм построения звездчатого многоугольника. Предположим, что мы строим звездчатый многоугольник, который должен содержать точки p₀, p₁,…, p_m–1. Центром тяжести точек p₀, p₁,…, p_m–1 называется точка p_C = (x_C, y_C), координаты которой равны 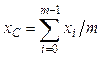, , 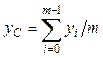где (x_i, y_i) — координаты точки p_i, а m — количество точек. Построим многоугольник, центр тяжести которого p = p_C принадлежит ядру.

С этой целью отсортируем точки p₀, p₁,…, p_m–1 по возрастанию угла наклона отрезков pp_i вокруг точки p. Соединяя затем p_i с p_i+1 , где p_m = p₀, для всех i = 0, 1,…m-1, получим искомый звездчатый многоугольник.

Приведем определение класса, объектами которого будут звездчатые многоугольники. Конструктор будет строить звездчатые многоугольники по описанному алгоритму.

Предположим, что структура точки состоит из двух полей, содержащих координаты точки, и всех необходимых для реализации алгоритма операций.

Определим класс звездчатого многоугольника.

class SPolygon

{

int color;                   // цвет области

int n;                       // число вершин

Point *p;                          // массив вершин

Point pC;                    // центр тяжести

public:

friend class Wnd;       // класс для вывода точек области на экран

SPolygon(float *x, float *y, int m, int cl);

};

SPolygon::SPolygon(float *x, float *y, int m, int cl)

:color(cl)                   // цвет

{

int i, j;

Point t;

n = m; pC.x = 0; pC.y = 0;

for(i = 0; i < m; i++)

{

pC.x += x[i]; pC.y += y[i];

p[i].x = x[i]; p[i].y = y[i];

}

// сортируем точки по возрастанию угла

// вокруг центра тяжести методом вставок

for(i = 1; i < m; i++)

{

t = p[i];

for(j = i - 1; (j >= 0) && ((t - pC) < (p[j] - pC)); j--)

p[j + 1] = p[j];

p[j + 1]=t;

}

}