Построение многоугольников и многогранников, страница 8

}

q[j] = p[i];

q[j + 1] = t;

delete []p;

p = new Pnt [j + 2]; n = j + 2;

for(i = 0; i < n; i++)

p[i] = q[i];

delete []q;

}

CPolygon(double *x, double *y, int m, TColor cl);

};

CPolygon::CPolygon(double *x, double *y, int m, TColor cl):SPolygon(cl)

{

// выпуклая оболочка методом Дейкстры

int i; Pnt t; p = new Pnt [3]; n = 3;

for(i = 0; i < 3; i++)

{

p[i].x = x[i]; p[i].y = y[i];

}

if((p[1] - p[0]) * (p[2] - p[1]) < 0)

{

t = p[1]; p[1] = p[2]; p[2] = t;

}

for(i = 3; i < m; i++)

{

t.x = x[i]; t.y = y[i];

Insert(t);

}

}

//--------------------------------------------------------------------------__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

double rad = 150;     //радиус окружности и вершины семиугольника

int i, mm = 7;

double *x, *y;

x = new double [2 * mm]; y = new double [2 * mm];

for(i = 0; i < mm; i++)

{

// вершины большого семиугольника

x[i] = rad * cos(2 * PI * i / mm);

y[i] = rad * sin(2 * PI * i / mm);

// вершины маленького семиугольника

x[i + mm] = rad * cos(2 * PI * i / mm + PI / mm) / 2;

y[i + mm] = rad * sin(2 * PI * i / mm + PI / mm) / 2;

}

randomize();

for(i = 0; i < 2 * mm; i++)

x[i] += random(100) - 50;

CPolygon dom2(x, y, 2 * mm, (TColor)RGB(0,200,200));       // построение выпуклой

// оболочки

SPolygon dom3(x, y, 2 * mm, (TColor)RGB(255,0,255));// построение звездчатого

// полигона

dom2.show(-300, -300, 300, 300);     // вывод выпуклой оболочки

dom3.show(-300, -300, 300, 300);     // вывод звездчатого полигона

}

//--------------------------------------------------------------------------В результате работы программы на экран будут выведены выпуклая оболочка 14 точек и звездчатый многоугольник, содержащий эти точки. На рис. 6.7 показаны примеры результатов вывода.

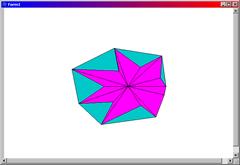
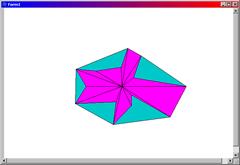
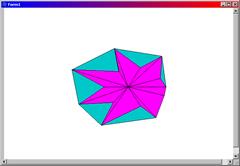
Рис. 6.7. Звездчатые многоугольники и их выпуклые оболочки

Выпуклая оболочка в трехмерном пространстве. Отметим, что рассмотренный выше алгоритм был предложен Дейкстрой для построения выпуклой оболочки в трехмерном пространстве. Он основан на приведенной ниже идее добавления точек к выпуклому многограннику.

Пусть многогранник P задан списком составляющих его граней. Построим список граней многогранника P', который будет выпуклой оболочкой вершин многогранника P и новой точки q, не принадлежащей P. Грани задаются как массив вершин соответствующих многоугольников. Грань называется видимой из точки q, если угол между ее вектором внешней нормали и вектором, соединяющим любую точку этой грани (рис. 6.8) с точкой q, меньше π / 2. В противном случае будем называть грань невидимой. Каждое ребро принадлежит некоторым двум граням. Мы будем допускать случаи, при которых две грани находятся в одной плоскости. Ребро, принадлежащее видимой грани и невидимой грани, называется контурным. Если соединить точку q с вершинами контурного ребра, то получится треугольник, который будет гранью многогранника P'. Следовательно, чтобы получить список граней многогранника P', нужно сначала удалить все видимые грани. Затем добавить к оставшемуся списку граней все треугольники, полученные соединением точки q с вершинами контурных ребер.

Рис. 6.8. Видимая из точки q грань

Пример 6.1. Построим выпуклую оболочку пяти точек, первые четыре из которых не лежат в одной плоскости. Обозначим эти пять точек через p₀, p₁, p₂, p₃, q. Перенесем начало координат в точку p₀. Поскольку точки p₀, p₁, p₂ и p₃ не лежат в одной плоскости, то вектора , ,  будут составлять базис пространства. Следовательно, существуют числа x, y, z, такие, что .

Рис. 6.9. Тетраэдр p₀p₁p₂p₃

Это равенство можно рассматривать как систему линейных уравнений с ненулевым определителем. Решая эту систему, сведем задачу к случаям расположения точки относительно тетраэдра, заданного системой неравенств: x ≥ 0, y ≥ 0, z ≥ 0, x + y + z ≤ 1 (рис. 6.9). Обозначим решение системы через (x, y, z). Возможны перечисленные ниже пятнадцать случаев, каждому из которых соответствует список граней выпуклой оболочки.