Построение многоугольников и многогранников, страница 15

if(((s[a] - s[k]) * (s[i] - s[k]) > 0.0) ||

((s[a] - s[k]) * (s[i] - s[k]) == 0.0 && fabs(s[a] - s[k])

< fabs(s[i] - s[k]))) a = i;

}

if(a == m) break;

}

n = j; p = new Pnt [n];

for(i = 0; i < n; i++) p[i] = pp[i];

delete []s; delete []pp;

}

int CPolygon::isin(Pnt t)

{

int i,j, parity = 0;

for(i = 0, j=n-1; i < n; j=i++)

{

if (( ( (p[i].y<=t.y)&&(t.y<p[j].y) )||

((p[j].y<=t.y)&&(t.y<p[i].y)))&&

(t.x<(p[j].x-p[i].x)*(t.y-p[i].y)/

(p[j].y-p[i].y)+p[i].x))

parity=1-parity;

}

return parity;

}

//--------------------------------------------------------------------------__fastcall TForm1::TForm1(TComponent* Owner): TForm(Owner)

{

randomize();

maxX= Form1->Image1->Width;

maxY= Form1->Image1->Height;

}

//--------------------------------------------------------------------------void __fastcall TForm1::Button1Click(TObject *Sender)

{

float rad = 150, *x, *y;             // радиус окружности и

// вершины 2mm-угольника

int i;

int mm = random(10)+2;

x = new float[2 * mm]; y = new float [2 * mm];

for(i = 0; i < mm; i++)

{

// вершины большого 2mm-угольника

x[i] = rad * cos(2. * PI * i / mm);

y[i] = rad * sin(2. * PI * i / mm);

// вершины маленького 2mm-угольника

x[i + mm] = rad * cos(2. * PI * i / mm + PI / mm) / 2;

y[i + mm] = rad * sin(2. * PI * i / mm + PI / mm) / 2;

}

for(i = 0; i < 2 * mm; i++) x[i] += random(100) - 50;

Form1->Image1->Canvas->FillRect(TRect(0,0,maxX,maxY));

CPolygon cpoly(x, y, 10, clLtGray);  // построение выпуклой оболочки

cpoly.show(-300, -300, 300, 300);    // вывод выпуклой оболочки

Form1->Image1->Canvas->Brush->Color = (TColor)clWhite;//восстановление кисти

Pnt f = {0., 0.};

for(i = 0; i < 2 * mm; i++)

{

f.x = x[i]; f.y = y[i];

if(cpoly.isin(f))

Form1->Image1->Canvas->Rectangle((int)(x[i] + 300.) * maxX / 600 - 1,

(int)((300. - y[i]) * maxY / 600 - 1),

(int)((x[i] + 300.) * maxX / 600) + 1,

(int)((300. - y[i]) * maxY / 600) + 1);

}

delete []x; delete []y;

}

//--------------------------------------------------------------------------Результат работы программыприведен на рис. 6.12.

   

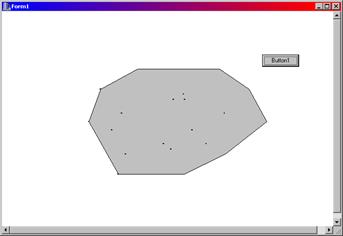
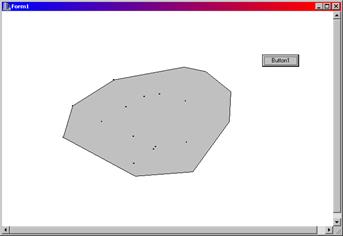
Рис. 6.12. Выпуклая оболочка, построенная методом заворачивания подарка

Оценим сложность алгоритма построения выпуклой оболочки методом заворачивания подарка.

Так как все m точек множества M могут быть вершинами его выпуклой оболочки, а рассматриваемый алгоритм затрачивает на нахождение каждой точки оболочки линейное время, то время выполнения в худшем случае равно O (m²). Если в действительности число вершин выпуклой оболочки равно h, то время выполнения алгоритма Джарвиса будет равно O (hm). Поэтому этот алгоритм особенно эффективен в тех случаях, когда заранее известно, что число сторон выпуклой оболочки ограничено некоторой константой h.

Метод обхода Грэхема. Этот метод основан на теореме о том, что последовательные вершины выпуклого многоугольника можно расположить в порядке, соответствующем возрастанию угла относительно любой внутренней точки. В качестве внутренней точки можно взять центр тяжести множества точек M, выпуклую оболочку которых требуется найти. Перейдем к системе координат с началом в этой внутренней точке. Упорядочим лексикографически все точки множества M в соответствии со значениями полярного угла и расстояния от начала координат. Сравнение расстояний выполняется лишь в случае, когда две точки имеют один и тот же полярный угол. В результате точки будут располагаться вокруг внутренней точки, как это показано на рис. 6.13. Легко видеть, что если точка из M не является вершиной выпуклой оболочки, то она будет внутренней для некоторого треугольника Opq, где p и q — последовательные вершины выпуклой оболочки.

Рис. 6.13. Метод обхода Грэхема