Проектирование установки для гидроиспытаний, страница 16

         Где Р(t) - давление в посудине, что меняется при вытекании.

Заметим,   что   из    этого     равнения       выплывает      закон      нарастания скорости в начальной стадии процесса, то есть когда P=P1 и 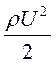<<P1,  что совпадает с выведенной раньше из рассмотрения волновой картины.

К давлений в несколько сотен атмосфер можно считать, что давление в посудине линейно связано с избыточным объемом жидкости  ΔV, что удерживается в этот момент в посудине.

Поэтому можем записать:

.

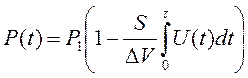       Подставивши последнее выражение в равнение (11) и перейдя   к

безразмерным переменного:

,

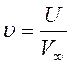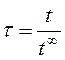
где  и   берем из (7.10) получим уравнение:

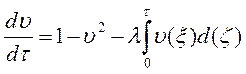, (7.12)

        где:                            ,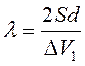

Для τ < 1 последним интегралом можно презреть и решение уравнения будет:

υ(τ)=thτ,   U(t)= th

В таблице 2 приведенные результаты численного решения равнения (7.12) при разных значениях λ:

λ	0	0,25	0,3	0,5	1,0	2,0	6,0
	1 1	0,74 0,86	0,71 0,84	0,60 0,78	0,46 0,68	0,32 0,57	0,14 0,37
	2	1,8	1,7	1,5	1,2	0,9	0,6
(l/d)m	1,3 0	2,08 0,47	1,9 0,48	1,6 0,48	1,08 0,46	0,68 0,40	0,29 0,25

7.3.4. Практический расчет защиты

Хотя в действительности при внезапном разрыве посудины форма отверстия, что образовалось, почти никогда не бывает круглой, стоит вести расчет для круглого отверстия, потому что можно показать, что наибольшую опасность представляет именно круглое отверстие.

 

Выражая в формулах (6) и (8) d через λ и Р_T через Р₁ посредством соотношений (7.13) и 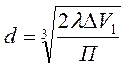(7.14):

,   (7.14)

Получаем соответственно:

δ>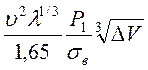,  (7.15) 

δ>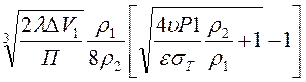,  (7.16)

Потому что для каждого Р₁   значения  зависит    от λ,    то необходимо подобрать такое значение λ, при котором правые части неравенств

(7.15) и (7.16) достигнут максимальной величины.

В формулу (7.15) входит произведение , из приведенной таблицы видим, что максимум этого произведения достигается при λ = 0,3 и близкий до 0,5.

Подставляя это значение в (7.15) для определения толщины защиты получаем:

δ>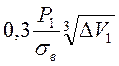 (7.17)  при  P1>, потому что при  λ = 0,3, = 0,7,    берется из формулы (7.9).

Для стали 3 формула (7.17) применимая при Р₁ > 30 МП а.

Для Р₁     < 30 МПа  нужно использовать формулу (7.16).

Ее применение усложняется тем, что λ, отвечает максимальному значению правой части,  зависит  от  Р₁,  поэтому  для  каждого  Р₁   необходимо

подбором находить такое  λ, которое дает максимум правой части неравенства.

При  этом  соответствующие  каждому  λ  значения    υ²    берутся из     таблицы. Однако расчет можно значительно упростить, если       воспользоваться    исходным    уравнением   (7.8), в котором  d  и  Р_T                        можно выразить через исходные параметры ΔV₁ и Р₁ из физических рассуждений.           

Действительно, при выводе формулы (7.8) выходили из импульса и энергии, что несет в себе часть струи длиной возле d/2 .

Очевидно, что эта энергия и импульс будут наибольшей в том случае, если главная часть несет в себе всю упругую энергию посудины с      жидкостью, ровную 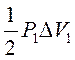   и  всю  избыточную  массу, ровную , то  есть если мы имеем, свойственно, даже не струю, а запятую жидкости, что имеет приблизительно одинаковые размеры во всех направлениях.

Тогда вместо (8) получим:

δ>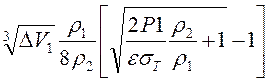,  (7.18)

В полученное выражение необходимо внести еще запас прочности, не меньше, чем 2,5.

Окончательная формула для расчета толщины защиты со стали Ст..5 ГОССТАНДАРТ 380-71 с коэффициентом запаса прочности

K=2,5;  σT=2900 кгс/см²   и   σБ=5000 кгс/см²   будет:

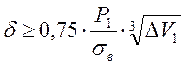 (7.19)

где величины параметров δ, Р₁, ΔV₁  имеют размерность: Р₁ — кГс/см , ΔV1 - см³,   δ - см.

       Расчет   ΔV1   для  сферических  и   цилиндровых   посудин  не  составляет