Механика \ Гидропривод и гидропневмоавтоматика

Проектирование установки для гидроиспытаний, страница 14

Рассмотрим взаимодействие струи с препятствием в предельных условиях, то есть будем допускать, что толщина δ именно такая, что лист в месте удара струи получает вмятину, но не рвется.

         

Взаимодействие распадается на два этапа:

1)  начальный процесс формирования течения на поверхности препятствия, когда в течение малого времени на препятствие действуют повышенные ударные тиски;

2)  занимающий все следующее время квазистационарный процесс взаимодействия, когда давление струи на препятствие определяется равнением Бернулли.

Рассмотрим эти стадии процесса отдельно.

II  стадия.    Полная  сила давления  струи  на препятствие равняется

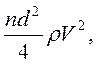давление в точке торможения на оси струи  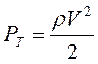          , поэтому

диаметр   области    высокого  давления ,  близкого  к    Рт  ,  на   поверхности препятствия будет приблизительно . По геометрическим рассуждениям                  отсюда  получается , что  радиус  кривизны  поверхностных  линий  тока   в области их поворота близкий  к  .

Равняясь центробежное давление поверхностного слоя струи, что имеет    скорость близкую к V, к давлению вблизи точки торможения, получим для этого слоя значения порядка .

После этого легко оценивается объем жидкости в околице точки торможения, что  имеет  давление  близкое к Рт   и  малую скорость; оно оказывается порядку .

Поскольку через малую сжимаемость воды упругая энергия жидкости в отмеченном объеме незначительна,  величина 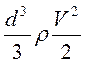   даст  нам  энергию,  что теряет струей при столкновении.

Эта величина нам будет нужна для рассмотрения 1-й стадии.

Дальше, подсчитаем растяжимые усилия на дне вмятины в II -й стадии.

Принимая, что поверхность вмятины сферическая, и что материал препятствия на всей поверхности вмятины тянется равномерно к предельно допустимому относительному удлинению, легко получить формулу, что связывает радиус кривизны поверхности вмятины R с ее диаметром dвм   и ε:

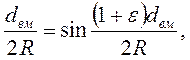 (7.1)

Диаметр вмятины должен быть близкий к диаметру области высокого давления, т.е.

 (7.2)

Решение равнения (7.1), в которое подставлены (7.2) для ряда значений данные в таблице 7.1.

Таблица 7.1                                  

ε

0,02

0,05

0,1

0,15

0,2

2,3

1,4

1,0

0,9

0,83

Видим, что для ε > 0,1, что отвечает конструкционным металлам,  слабо зависит от ε, поэтому в дальнейшем будем думать, что:

R=d,  (7.3)

За условия << 1 ,   что, как будет видно далее, при давлениях до нескольких сотен атмосфер, достаточно хорошо выполняется, стенку вмятины можно считать тонкостенной, а напряжение σ, что растягивает, в ней рассчитывать по формуле:

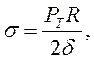 (7.4)

Очевидно, что σ  не  должно  превышать  эквивалентного  напряжения что

расторгает, при двоосевом растягивании:

σ<, (7.5)

Соединяя формулу (7.3-5), получим условие того, что стенка выдержит напор постоянной струи, в виде:

δ>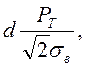  (7.6)

Теперь нужно выяснить, выдержит ли защиту бронекамера, рассчитанная по формуле (7.6), влияние струи в I стадии.

Перед моментом столкновения все части жидкости двигаются перпендикулярно поверхности препятствия со скоростью V.

После столкновения боковая поверхность струи вблизи препятствия получает ту же скорость V в перпендикулярном направлении в результате действия боковой волны разжижения на сжатое, что образовалась ударной волной жидкость.

Повышение давления действует на препятствие до тех пор, пока струя растечется вдоль поверхности препятствия к окружности диаметром порядка 2d, потому что к этому моменту распределение скоростей в струе в околице точки столкновения приблизится до распределения при стационарном обтекании.

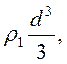На этот процесс расходуется отрезок струи длиной возле , что имеет массу ~  импульсом ~  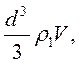и энергией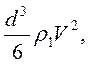

Отметим, что оценка объема и энергии этого отрезка струи дает ту же величину, что была получена раньше другим путем, для объема и потери энергии заторможенной жидкости при постоянном обтекании.

Скачать файл